Appendix: Calculating a planet’s temperature
Here we’ll go into some significant algebra and simple geometry but no calculus. We’ll consider a stellar system (analog of our Solar System), with a central star at a known temperature, Ts, and a size described by its radius, rs. It has a planet at a distance or orbital radius, ro, and this planet has its own radius, rp. We’ll assume a perfectly circular orbit, which only a few planets follow. The changes in energy balance within an elliptical orbit are a topic for another section.
DIAGRAM
At the surface of the star, that is, at a distance rs from the star’s center, there is an enormous energy flux density (energy per unit area per unit time, in watts per square meter),
As noted earlier, σ is the universal Stefan-Boltmzmann constant. It has a magnitude 5.67×10-8 watts per square meter per Kelvin to the 4th power. This magnitude will actually be irrelevant here, since it cancels out on both sides of the relevant equations.
The stellar radiation spreads out at distances from the star’s surface, decreasing in proportion to one over the square of the distance, r, from the star’s center. That’s easily shown with geometry: the total radiation leaving the star is its density per area multiplied by the star’s surface area, Irs2. That has to be the same as the total radiation reaching any distance r, since there are no sources nor losses of energy along the way. Writing the energy flux density at distance r as Ir, we have
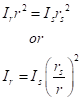
As a touchstone, consider our own Sun, which has a temperature of 5800 Kelvin and a corresponding Is= 64 million watts per square meter (the 64,000 hair-dryer units). Its radius in 696,000 km, and we sit on Earth at a distance of close to 150,000,000 km, on average. That gives a reduction of intensity by a factor of (0.696/150)^2, or about 22 parts in a million, to a value Ir = 1380 watts per square meter.
The energy burden on the planet is proportional to the fraction of the solar energy absorbed; we’ll call this factor a. That’s about 71%, or 0.71, given reflections by clouds and some multiple encounters. This is at the top of the atmosphere, TOA. At the surface, the greenhouse effect enters, and we deal with that elsewhere.
At the Earth’s frontal area (seen perpendicular to the direction of sunlight) of πrp2, the average rate of absorption of solar energy is that area multiplied by Ir at Earth’s distance and multiplied again by a. Now, since the Earth rotates, it spreads the energy over its total surface area that’s four times larger, 4πrp2. So, the average rate at which the Earth’s surface absorbs solar energy is
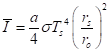
To deduce the TOA temperature, or radiative temperature, of the Earth, we equate this to the energy flux density that the Earth has to radiate back out to space, as thermal infrared radiation. That’s the same type of formula as for the Sun,
We can equate the two formulas for to get
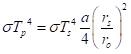
Let’s cancel out the sigmas and take the fourth root to get Tp directly:
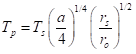
Several things are clear:
- The temperature of the planet is simply proportional to the temperature of the star. They share the same physics of thermal radiation
- Temperature increases with fraction of stellar energy absorbed, a, but weakly
- The remaining factor is pure geometry, the square root of the ratio between the star size and the orbital size
Checking this our for the Earth, we get
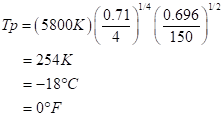
That’s the actual view from space. We look very cold. The greenhouse effect boost us by 33°C to +15°C.
The calculations and measurements for the other planets in our Solar System are given in the text. They show the expected wide variations, from hot Mercury to cryogenic outer planets with temperatures of liquid methane, liquid nitrogen, even nitrogen slush.
Planets around other stars
Now let’s consider a different star, such as exobiologists talk about for looking for signs of life or for (rather preposterously) colonizing. This star will have a different mass, Ms, compared with the mass MSun, and a different surface temperature, Ts, and a different size or radius, rs, with a correspondingly different mean density, ρs. There are a number of considerations:
- A hotter star requires a greater stand-off or orbital distance to reach an equable planetary temperature
- A larger star also requires a greater stand-off distance; we have to keep rs/ro constant, for the same star temperature
- More massive stars at the same temperature and the same orbital distance generate a faster orbit for the planet and a greater gravitational force at the planet, hence, a greater tidal bulge. If strong enough, that could lead to tidal locking of the planet’s rotation on its own axis. The bulge becomes a big handle for the star to grab, as it were.
- There is one tiny, cool star, Proxima Centauri b, briefly considered as having a planet in its habitable zone by virtue of estimated temperature only. A cool star must be orbited at a smaller distance. A star that’s also small in radius must also be orbited at a smaller distance. Even with a lower stellar mass, the tight orbit gives a high gravitational acceleration and tidal bulge.
The first step is to calculate the orbital distance from the balance of gravitational force with the effective centrifugal force. Newton gave us a nice formula for the gravitational force in terms of the stellar mass, the planetary mass, mp, the orbital distance, ro, and a universal gravitational constant, G:
The centrifugal force is likely familiar to a number of readers. For a planet in a circular orbit moving at a speed vp, it is just
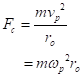
In the second line I rewrote the speed in terms of its angular speed, ωp = vp/ro. That’s the number of radians (arcs as long as the radius of the orbit) traversed per unit time.
I ignore the tiny effect that the planet and the star actually orbit around their center of mass; it’s very close to the center of the star because stars are so much more massive than their planets. If you’re curious about the form of the centrifugal force, you can see a post.
Balancing the two forces, we get
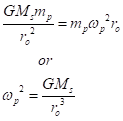
If we fix the planet’s orbit to get the right planetary temperature, a more massive star gives us a faster angular velocity, ωp, and, thus, a shorter orbital period. Since one orbit is 2π radians, the period of revolution around the star is
This is Johannes Kepler’s famous formula from around 1600 CE. The period is shorter in proportion to one over the square root of the star’s mass. It is also proportional to the 3/2 power of the orbital radius – outer planets take longer to orbit the Sun here in our Solar System. It’s more than simply proportional to the circumference of the orbit, because the more distant planets move at a slower speed, proportional to one over the square root of their distance.
In any event, if all else is equal, a more massive star with the same absolute size (radius, rs) and temperature only requires the same orbital distance but a higher speed in orbit. That does influence the gravitational acceleration, g, felt at the planet along the line toward the star,
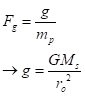
We feel this but little in our Solar System as the direct pull on us from the Sun relative to the pull from Earth’s own mass. A quick calculation of the relative effect on us of the Sun vs. the Earth is
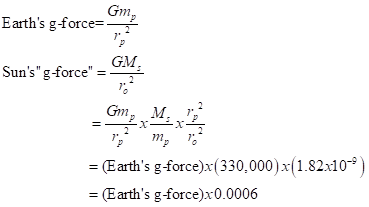
The difference (or gradient, the derivative with respect to distance) of this force across the planet makes a bulge in the Earth, both is oceans and in nicely elastic and deformable solid rock. Interestingly, the bulge is both directly toward the Sun and, in equal amount, directly away from the Sun. The proof of this is interesting, in a separate post. Actually, I oversimplified. The bulges from both the Sun and the Moon are ahead of the directions toward these bodies because the oceans slosh like water in a pan that you’re carrying. It’s easy to prove to yourself by carrying water and skipping the precaution of not looking at the water. Your eye-limb feedback results in a slosh that’s maximal not where your relative to- or fro- motion is maximal but in between. In the main text we explore the effect of this offset to note how the Moon pulls back on this bulge and end up slowing down the Earth’s rotation markedly over the eons (by more than a factor of two!) and also distancing itself from Earth (giving us the perfect relative Sun-Moon distances that we can see both solar and lunar eclipses!). My wife and I became acutely aware of the lag when we were in Kenya in 1980 for travel at the time of a solar eclipse. After watching colleagues launch a sounding rocket that tried to observe the eclipse (alas, there was a guidance error), we thought we might go snorkeling, even though the Sun’s pull would likely raise the depth of water a good deal, making it more of an effort to get down toward the bottom. In fact, the ocean level was at an all-time low; corals were sticking out of the water for hours
Finding a planet with Earthlike temperature but around a different star
Now consider a star of a different temperature, Ts, while we wish to find an orbital radius that will make for a comfortable planetary temperature – say, a radiative temperature of 254K, as for Earth. We have shown above the relationship
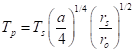
Let’s fix Tp where we want it and figure out what orbital distance, ro, we want:
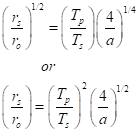
We know how this worked out for the Sun – Earth system, with
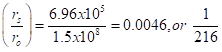
That is, the Earth’s orbital radius is 216 times the Sun’s radius. This matches what we calculate for the right-hand side of the equation,
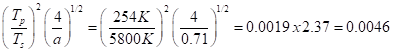
If Ts is higher, then ro has to be larger, getting farther from the fire, as it were. It has to be greater by the ratio
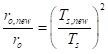
So, a planet around a star that’s 50% hotter than the Sun, Ts,new = 1.5 Ts, has to be 1.52 = 2.25 times farther away. Another case is a star that’s the same temperature as the Sun but bigger. The right-hand side of the earlier equation is the same, so rs/ro has to stay the same. With a star 50% larger than the Sun, the planet has to be 1.5 times farther away.
It’s more likely that we want to find a star that’s no hotter than the Sun, to avoid excess ultraviolet light intensity. In another appendix, I show how to calculate the fraction of radiation in the UV waveband, as a function of star temperature. For the Sun, there’s about 3% as much UV radiation as in the visible range. That much UV can be nicely shielded by our ozone layer. For a star 50% hotter, at Ts = 8700K, there’s about 100% as much UV as visible! That’s a deal-breaker for life around that star, barring some very weird physics and chemistry of the atmosphere.
So, consider a cooler star, and, while we’re at it, a smaller and denser star, Proxima Centauri b. It has a temperature measured at 3042K, or 0.52 that of the Sun. It is small, having a radius that’s only a bit bigger than that of the Sun, or about 0.15 times that. It’s 33 times as dense as the Sun but has a mass only 0.12 times that of the Sun. Now, we’ll assume that the same fraction of energy flux is absorbed as on Earth, 71% (even though the absorbing compounds would have to be different for the very different wavelengths that dominate). Now we may calculate the orbital radius for a “nice, warm” planet around this star. We use an earlier equation to get:
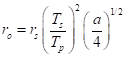
We can plug in numerical values to get an answer of 6.24 million km, or 4% of Earth’s orbital radius. It may be of more interest to develop a general formula that compares the orbital size to that of Earth around our Sun:
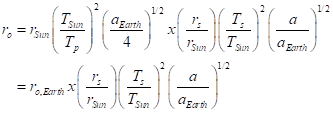
The second line shows how three different factors affect the orbital radius required to get the planet to have the radiative temperature, Tp, of Earth. For Proxima Centauri b, the first factor is 0.15, since the star is small. The second factor is 0.272 because the star is cool. In the absence of direct information, I assume that the second factor is unity. This gives a “contraction” factor of 0.042. It’s a really tight orbit.
BALANCE FOR PLANETS IN OUR SOLAR SYSTEM!
Tidal locking of a planet around a star
There are major consequences of a tight orbit, one of which is a strong gravitational distortion or bulge on the planet that can lead to tidal locking – the bulge of the planet is so pronounced that the star pulls the planet along in a fixed orientation relative to the star; the same face on the planet always faces the star. Our own Moon is tidally locked to Earth, so that, apart from glimpses of the edges caused by wiggles or librations of the Moon, its far side was only seen remotely by spacecraft, beginning with the 7 October 1959 flight of the Soviet spacecraft Luna 3.
We can compute the gravitational acceleration (gravitational force per unit mass) experienced by the planet simply, as
Again, we can plug in numerical values, but an interesting comparison is this strength relative to the gravitational acceleration we feel from the Sun on Earth (note that this is quite small compared to the gravitational acceleration we feel from Earth’s mass, only 0.06% as strong). Actually, let’s skip to the gradient of the gravitational acceleration, which is the rate of change of the acceleration with distance from the star. This causes tides, or tidal bulges, in the water and rock on any planet. The formula is
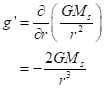
The notation ∂/∂r is from calculus, indicating that the quantity after the symbol is being differentiated, that is, taking the difference between its value at two nearby locations and dividing that by the small difference in locations (r). If we’re drawing a curve of g versus r, this is the slope.
To continue, we’ll compare this to the gravitational gradient at Earth from the pull of the Sun:
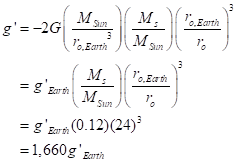
That’s a whopping tide. The “Earthlike” planet around Proxmina Centauri b is certainly tidally locked. Let’s explore this:
Temperatures on a tidally locked planet or any planet facing a star for long periods
In the simplest view, a part of a planet facing a star without fast enough rotation to average out temperatures will have four times the rate of radiation absorption as that same planet, were it to rotate. Given that the fourth power of absolute temperature scales with this irradiance, the temperature rises to 40.25 = 1.41 times that on a rotating planet. For Earth, keeping the same cloudiness level (not really possible), that would be 359K, which is 86°C or 187°F. The cold side cools radiatively to outer space, which is around 3K, or -270°C. Mercury rotates very slowly, with the hot side attaining 460°C and the cold side attaining -180°C. Note that the cold side doesn’t reach 3K because of stored heat being slowly released.
Let’s go back to Proxima Centauri b, figuratively. Just based on radiative energy balance, we may figure out where the temperatures are consistent with life. I’ll make some simplifying assumptions. For one, I’ll assume that the temperature of a location on the planet depends upon the amount of stellar radiation at that point, plus an increase from a greenhouse effect. This means not accounting for heat being transported to or from this spot by an atmosphere or ocean such as happens on Earth (which is why the poles are not even colder and the equator even hotter than they are). Now, the amount of radiation will depend on the angle between the direction to the star and the normal or perpendicular to the surface (for flat areas). Thus, we’re going to calculate a range of angles that make the radiation not too low, not too high, just right, a Goldilocks story. We’ll use the estimated energy flux density from the star at the planet’s orbital distance of 6.4 million km. That value is readily calculated from formulas much as give above as 1210 watts per square meter.
Let’s start with the highest temperature consistent with at least microbial life, 70⁰C or 343K. How much absorbed radiation will support this as a steady temperature? First, may we assume that there is no significant greenhouse effect? Oops, that’s not possible. If there’s water, there’s a strong greenhouse effect. I’ll use an Earth-like greenhouse effect that raises temperatures by 33⁰C . So, the radiative temperature of a location should be 33⁰C lower than the surface temperature. Our higher surface temperature of 70⁰C corresponds to a radiative temperature of 37⁰C or 310K. We’ll use the blackbody equation again, I = σT4. We obtain I = 524 W m-2, which is 43% of the direct starlight intensity. This occurs at an angle away from the central star, “PCb,” of 64⁰.
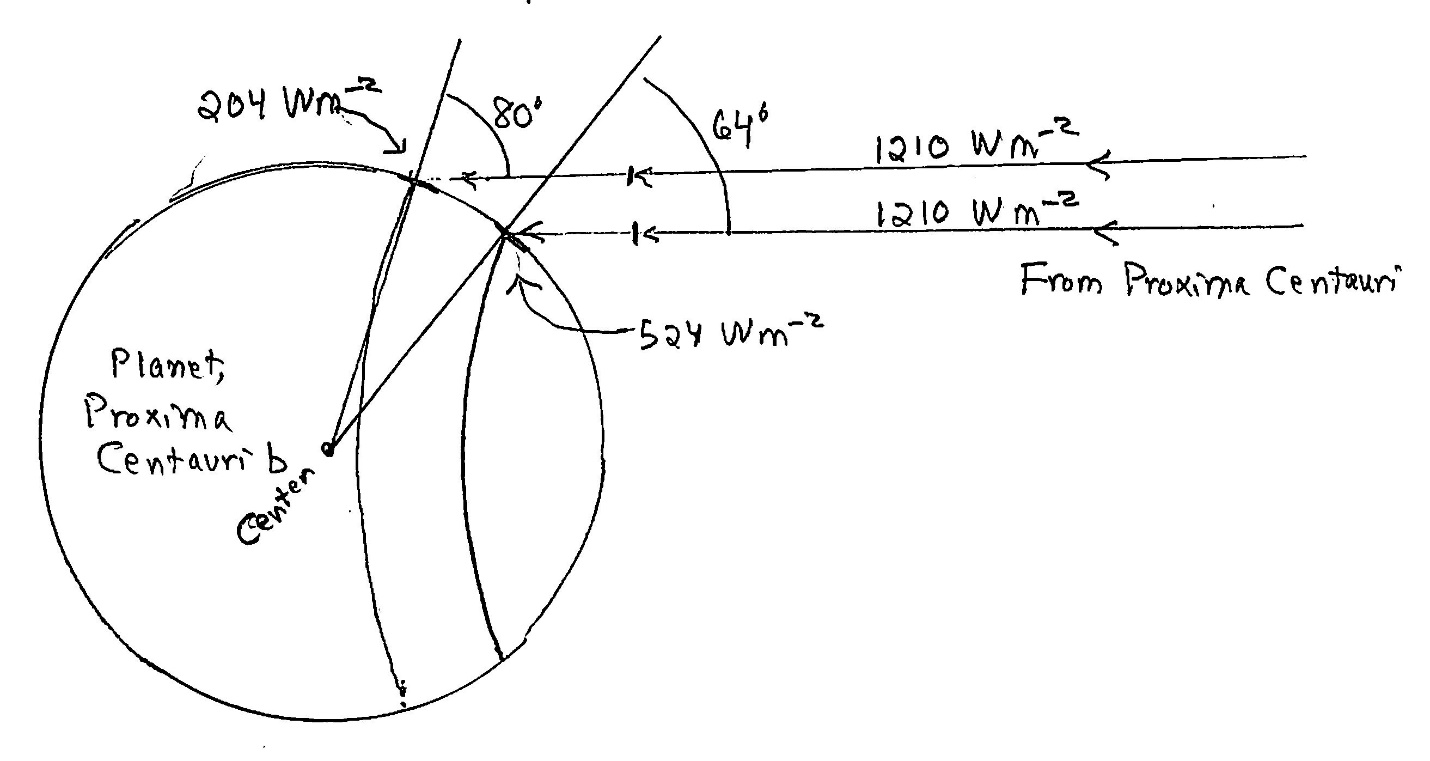That’s over 2/3 of the way, in angle, to the “terminator,” or permanent shadow zone that starts at what we might call the equator. Let’s proceed to the lower temperature. I’ll take this as 5⁰C. Yes, I know that bacteria on Earth are found in areas that get seasonally much colder. However, on a tidally locked planet we don’t expect changeable weather; each location stays around its own constant temperature (except when the star flares!). At a surface temperature of 5⁰C, the radiative temperature will be 33⁰C lower, or -28⁰C, which is 245K. For this, we need an energy flux density I = 204 W m-2, which is 17% of the full starlight. This occurs at an angle of about 80⁰ from overhead, almost to the planet’s terminator or equator. Overall then, my first estimate is that there’s a narrow band of angles on the starlit side that’s habitable, from 64⁰ to 80⁰. By geometry, we can figure out that this covers a fraction (0.43-0.17)/2 = 13% of the planet’s surface.
Alas, this won’t work. On the colder side, temperatures reach way below the freezing point of water and, in fact, even carbon dioxide. There’s no significant greenhouse effect from the refractory gases left, that, using some imagination, might include oxygen. Natural convective motion of gases would move the water and CO2 inexorably to the cold side, permanently locking them up there. A local demonstration of such an effect is on Mars, where CO2 condenses into dry-ice caps on the poles.
One last bit: temperature of an surface with no illumination but a geothermal heat flow
This is fast. Let’s take a notional example of Earth, with a mean heat flux from its interior of Ig = 0.06 watts per square meter. Let this be balanced by thermal radiation leaving the surface. As earlier, the balance is
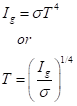
I’ve ignored any deviation from perfect emissivity, which deviations would give a higher kinetic temperature; this is an equation solely for the radiative temperature such as an alien in a spaceship might measure remotely. Plugging in the numbers gives us 32K or -241⁰C. This is surprisingly warm, and it comes from that weak ¼-power dependence of temperature upon energy flow. Some of our own Solar System planets are warmer than expected from their puny solar irradiation because they have hot interiors and resultant geothermal energy flows. Note that the rise in temperature is not additive with the temperature from solar radiation; both geothermal and radiant energy inputs add inside the numerator above. When radiation is higher than geothermal energy flow, the latter barely matters, as is evident with a little math.
Final comments
There are many interesting inquiries to follow up – how we measure the temperature of the Sun or any other star, its radius, our distance from it, the average fraction of energy absorbed, our own radius. The history of how these measurements have been and are being done is for another session.