Centrifugal force: its effects on our weight and on the shape of the Earth
Vince Gutschick, Las Cruces Academy, Inc. and Global Change Consulting Consortium, Inc.
The basics of centrifugal force
Simple case: assume that the Earth is a true sphere. Evaluate the effect of centrifugal force from the Earth’s rotation on our weight (not our mass, of course). This is a common exercise, and a good start.
Gravitational force on a mass m anywhere on this spherical Earth (which is also assumed to be uniform laterally or by lat/long, even if uneven by depth):
![]()
Here, G is the universal gravitational constant, 6.67384 × 10-11 m3 kg-1 s-2, M is the mass of the Earth, 5.972 x 1024 kg, g0 is the basic surface gravitational acceleration, 9.8 m s-2, and the first formulation uses the fundamental law of gravity for the gravitational force between two objects of mass M (the Earth’s mass, in our case) and mass m (us), when their centers of gravity are separated by a distance r. For objects that are spherically symmetric (density varies with depth but not laterally), the centers of mass are simply their geometric centers, by a nice theorem that I won’t prove here.
Now consider the Earth’s rotation about its own axis. The centrifugal force on something moving with the surface of the Earth at a tangential velocity v and a distance r from the axis of rotation, is exerted outward and it has the magnitude
![]()
The hand-drawn sketches below give quick derivations of this formula, by two complementary approaches. In both cases, we’re looking down on an orbiting object, viewing down the axis of rotation. Here is the first figure:
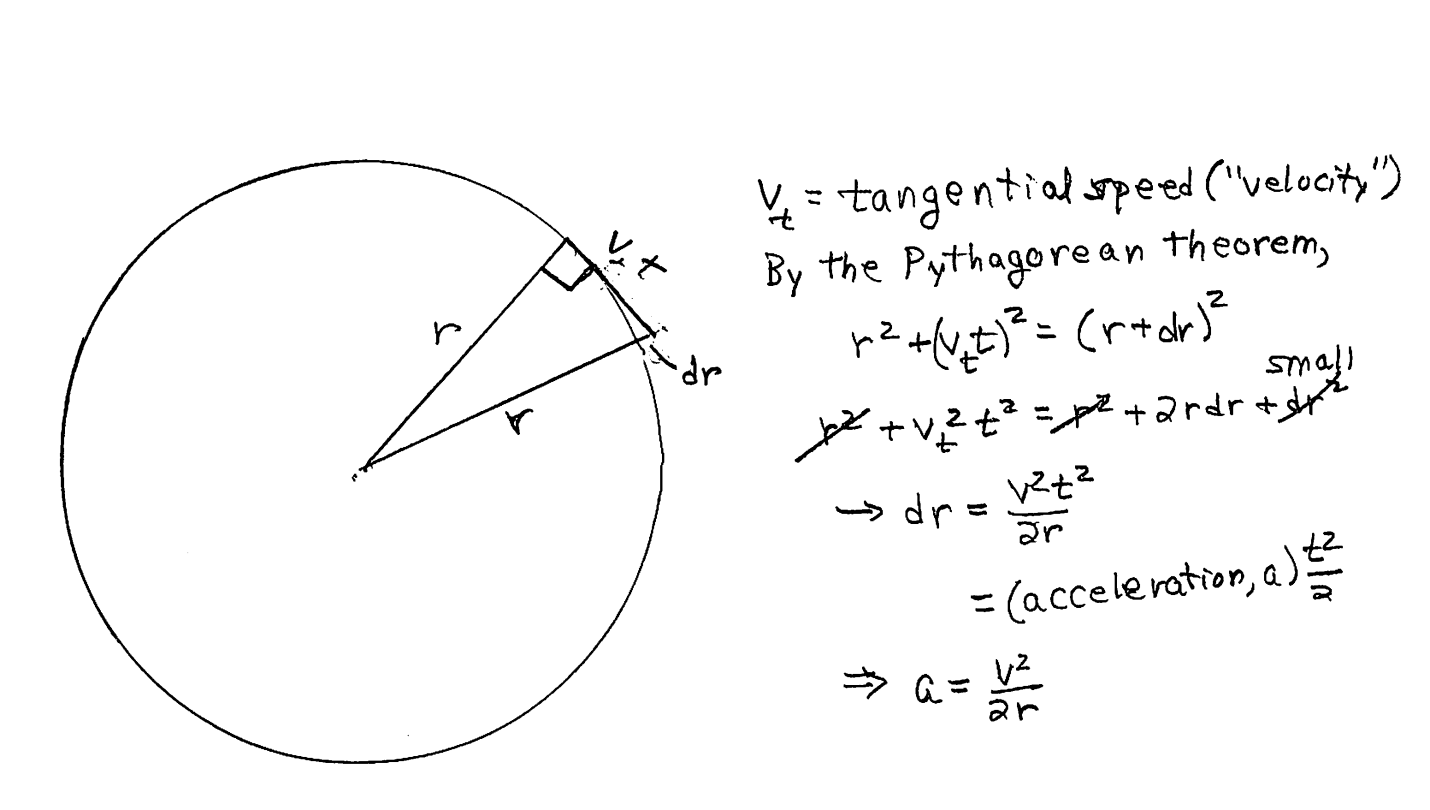
In a time t the object moves a distance vtt , where vt is the tangential speed, loosely called velocity (velocity is properly a vector, a speed with a specified direction). If the object were to continue in a straight line, as it would if no force acted on it, it would end up at the location shown, and thus be at a larger distance, r+dr, from the center of the orbit. We use the Pythagorean theorem to relate dr to the speed, time, and distance, to get dr= ½ (vt2/r)t2. The object has to be pulled in by this distance, by a force (a tether, or gravity). A force with a constant acceleration, a, pulls an object by a distance ½ at2. Centrifugal acceleration pushing outward balances this other acceleration, so that the centrifugal acceleration has the magnitude v2/r, and the force is this acceleration multiplied by the mass of the object, or just mv2/r, as above. Of course, centrifugal force is a construct, not a real force, arising because we’re trying to explain motion in an accelerated frame of reference, not an inertial frame.
In this second sketch, we look at velocity vectors. ![]()
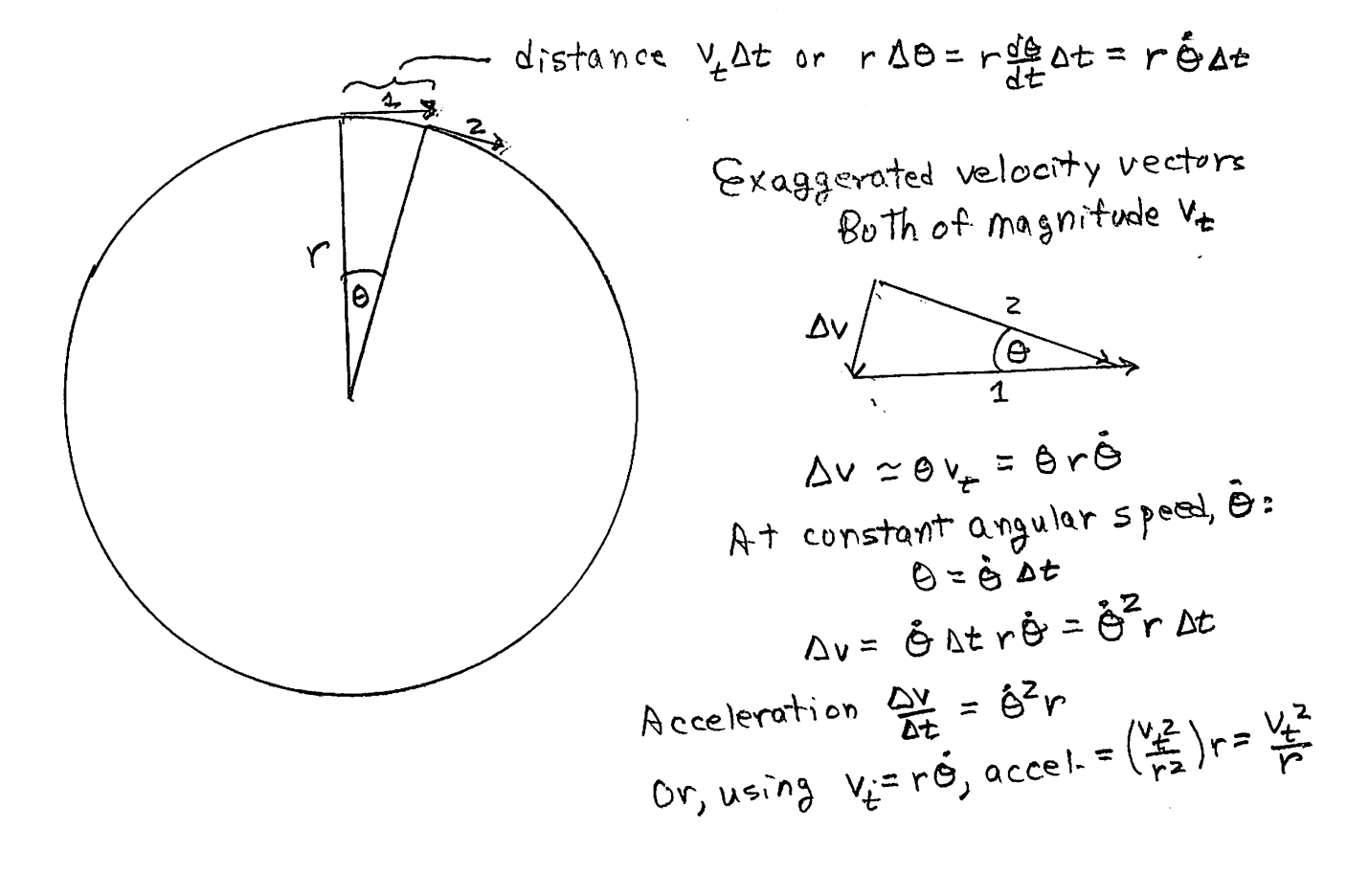
The object is rotating at a constant angular speed, dθ/dt. Measuring angles in radians, the distance that the object moves in a short time Δt is the chord of the circle, rθ, which is just r (dθ/dt) Δt. Having moved this distance, the object has a new velocity vector pointed in a slightly different direction. On the right of the circular orbit, we carry out the math to resolve the new velocity vector as the old one with an added velocity shift, Δv. By the math that follows, we see that the centrifugal acceleration is (dθ/dt)2r or vt2/r. Here, the subscript “t” means “tangential” (to the orbit).
How centrifugal force affects the apparent force of gravity
A third sketch here gives the apparent effect on gravity, a reduction of the acceleration of gravity by the centrifugal acceleration. (Of course, centrifugal force is a fictitious force resulting from viewing things in a rotating and therefore angularly accelerating frame of reference; you can look this up.)
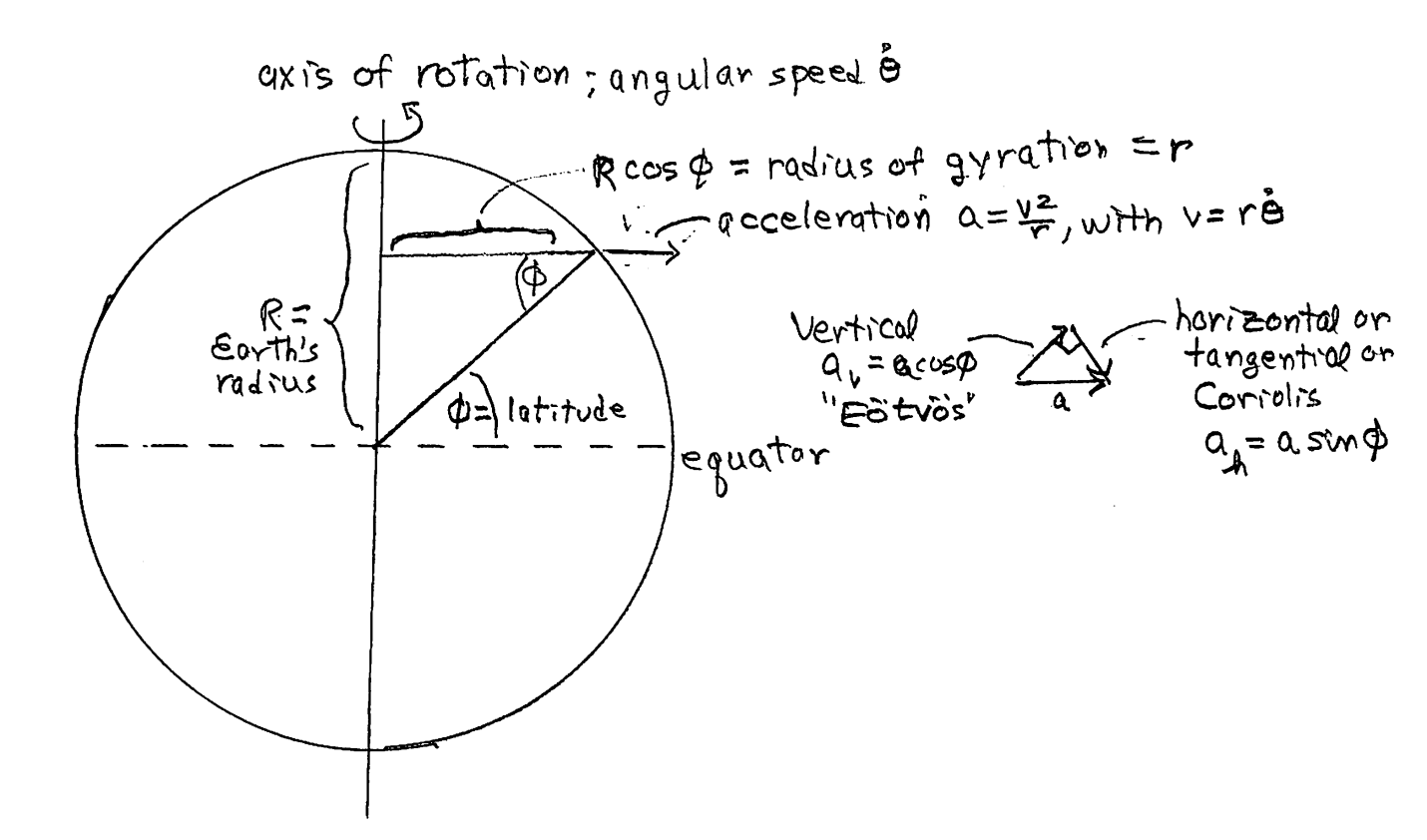
Now we’re looking sideways at the Earth. Some object (maybe one of us) is stationary with respect to the Earth at a latitude φ. As the Earth rotates, the object rotates at a distance r = R cos(φ) from the axis of rotation. We call this distance the radius of gyration. The object feels a centrifugal acceleration of magnitude a = v2/r. The velocity can be expressed as r(dθ/dt), with (dθ/dt) being the angular speed of the Earth’s rotation, which we’ll calculate shortly. We’re measuring angles in radians here, by the way, not degrees; 2π radians equals 360°, making a radian about 57.29°. A radian is the angle that gives an arc with the same length as the radius of the circle on which the angle is measured. To continue, we have by geometry that v =R cos(φ) and also r = R cos(φ), so that the acceleration a =v2/r is (dθ/dt)2R cos(φ). Now, the acceleration is not directed perpendicular to the Earth’s surface. Rather, it points perpendicular to the axis of rotation, or parallel to the equator. We can resolve the acceleration vector into two components, one perpendicular to the local surface of the Earth (local “vertical”), and one tangential to the surface. The local vertical component, a sort of anti-gravity, has the magnitude a cos(φ), or
(dθ/dt)2R cos2(φ). At the equator, cos(φ) is 1, and the vertical outward acceleration is maximal, with magnitude 2R 2. At the poles, cos(φ) is zero, and there’s no centrifugal acceleration. Note that the tangential acceleration gives the so-called Coriolis force.
We can calculate some magnitudes. We need the radius of the Earth, R, and its angular velocity. The radius varies a bit with latitude, mostly (the Earth is a prolate spheroid because of these centrifugal forces!), with an average value of 6371 km = 6.371 x 106 m, to put it into SI units. It rotates to face the Sun at the same point in 24 hours, but that is the time of rotation in a space-fixed frame (relative to the distant stars, an inertial frame of reference), plus a few extra minutes to turn a bit more to face the Sun as the Earth has advanced in its orbit around the Sun. OK, this is a bit picky, but the sidereal time (for one rotation relative to the “fixed” stars) is 23 h, 56 min, 4.09 s (and taking a bit longer all the time, as the Earth’s rotation slows; the Moon pulls on the Earth’s tidal bulge). Let’s take the rotation period then as 86164 s. The angular velocity, (dθ/dt) , is then, in radians per second, 2π / 86164 s = 7.2921 x 10-5 s-1, because the Earth moves through 360 degrees or 2π radians in that time.
At the equator, where the centrifugal force is straight outward / upward, opposing gravity, the centrifugal acceleration is
![]()
This is 1/289th of the standard force of gravity. If you weigh a “real” 70 kg, you weigh less at the equator by 0.24 kg. Feel better, lighter, healthier?
At other latitudes, specified by angle φ, while still assuming a truly spherical Earth, the vertical part of the centrifugal force, or Eötvös effect force, is smaller than this by a factor of cos2(φ) , as shown above. At, say, 45° N or S latitude, cos(φ) is 1/ = 0.707…, and cos2(φ) is just ½, so that you only feel ½ as much reduction of weight.
The Earth is flattened at the poles and this affects the perception of gravity
The Earth is flattened by the same centrifugal forces that act on you or me. Thus, the radius of the Earth at the poles is an average of only 6356.8 km and at the equator it’s 6378.1 km (I say “average” or mean, because there are nonuniformities in the distribution of mass, such as oceans and mountains). That means that, at the equator, you have another factor reducing your weight; you’re farther from the center of gravity of the earth. We can see from the first equation in this document that the force of gravity varies as 1/R2. You are now farther away than the mean radius by a factor (6378.1/6371) = 1+0.001114, so pure gravity is less by a factor 1/1.001142. You can do the math, using 1/(1+x) as being close to 1-x, to get a reduction by a fraction 0.0023, or another 1/448th of average pure gravity. There’s another 0.16 kg weight loss for a 70 kg “you.”
Centrifugal force also flattens the Earth from equator to poles
OK, all the rocks and such on the Earth “feel” the centrifugal force. Over the long term, rocks can deform under forces like very viscous liquids (that’s what plate tectonics is all about!). So, let’s calculate what shape the Earth should take if the parts of the Earth at the surface have the same total potential energy, comprised of the gravitational potential energy and an effective centrifugal potential energy. The argument about the parts having the same total energy is simply stating that, if they did not, mass would flow from one latitude to another, which is not the long-term pattern; tectonic plates do move, but the motion is from convective forces, not centrifugal force.
The gravitational potential energy is simply the form that is consistent with the gravitational force. Now, force, for a conservative force (one not depending on velocity, only on current state or locations), is just the derivative of the potential that is the source of the forces when one changes distances. If gravitational force is –GMm/R2, this comes from a gravitational potential Vg that is +GMm/R. One can readily take the derivative, dVg/dR to find that the force is –GMm/R2.
The effective centrifugal potential, Vc, is one whose derivative, dVc/dR, is the form we derived above. On a roundish Earth, the force is
![]()
The sign is positive; the force is directed outward, toward greater values of R. A potential that would give this force is simply
![]()
If you take the derivative, dVc/dr, you retrieve the form of Fc above.
Now, we want to say that the sum of the potentials, Vg + Vc , is the same at the poles and the equator, so that we can predict the flattening. We’ll let the radius of the Earth at the poles be Rp and the radius at the equator be Re = Rp + ΔR. We then want this equation to be true (removing the mass factor, m):
![]()
We’ve used the fact that cos(φ)=1 at the equator in the last term.
We’ll use the smallness of ΔR relative to R to expand the two terms on the right side and throw away the higher-order terms. We use these relations:
![]()
and
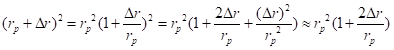
We can rewrite the equation for equality of total potentials to be
At the poles = At the equator
![]()
We can cancel the factor GM/Rp that occurs on both sides and then move terms to get
![]()
We can even neglect the final term, 2ΔR/Rp as a higher-order correction to get
![]()
We can plug in the values of the universal gravitational constant, the mass of the Earth, the polar radius, and the angular velocity of the Earth’s rotation on its axis to solve for ΔR. Rather than track down the values of G and M, we can use the simple relation that GM/Rp2 is just the usual gravitational acceleration at the Earth’s surface, g (or very close to it, ignoring the slight difference between the value at the poles and the average value). Thus, we can write
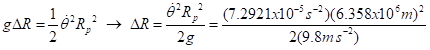
This gives
![]()
The actual value is 13 km, so this is pretty close. Rocks really do deform like this.
A few more interesting notes about centrifugal force and gravity, among many!
There are many additional interesting things about centrifugal forces and the shape of the Earth. For example, the Coriolis force generates cyclonic and anticyclonic air circulation, including hurricanes. Also, the very detailed deformation of the Earth has been measured by various means, with a new one being the Gravity Recovery and Climate Experiment (GRACE). In this observational experiment, two satellites follow each other about 220 km apart, with their distance apart measured by lasers with extreme precision, down to about 10 micrometers, less than 1/5 the diameter of a human hair. Now suppose the lead satellite approaches an anomalously large mass on the Earth below. It speeds up and increases its distance from the trailing satellite. Then, as it goes past the mass, it’s pulled backwards, while the the trailing satellite is speeded up, so that the distance between them decreases. With a continuous record of these small distance changes, the system can estimate the variations is mass distribution on the Earth. The satellites are in polar orbits, so their paths precess in longitude, allowing sampling of the whole Earth’s surface repeatedly. GRACE can detect not only static anomalies such as mountains (which other methods do on a finer spatial scale) but also dynamic changes – the melting of ice in glaciers and Antarctica and Greenland, the depletion of groundwater in India and the Middle East by irrigation pumping, and even the rain that fell on the Western US after a series of storms! All this is done from 500 km up…and it’s being repeated by two satellites orbiting the Moon, mapping its gravitational field and detailed shape!