Addressing a paradox: do you weigh less at noon than at midnight because you’re closer to the Sun, which then exerts more pull on you up from the Earth’s surface?
This is problem number 17 on page 362 of an older edition of Physics, Parts I and II, Combined, 3rd Ed., Resnick and Halliday (Wiley & Sons, NY, 1978).
I noodled over this, and looked up answers given on websites, all of them oversimplified and incomplete. One such argument is that the bulge is symmetrical, the same amount on the side of the Earth nearest the Sun and on the side farthest from the Sun. The arguments says that the pieces of the Earth, particularly those at the very surface, bulge out the same, so that gravitational forces felt on Earth must be identically inward on both sides.
The equality of the bulge can be measured nowadays, but it’s not obvious from first principles. So, I worked it out, with two simplifying assumptions, one that certainly doesn’t change the result: (1) the Earth is not rotating relative to the axis to the Sun – the extra centrifugal force of the Earth’s rotation is a constant, anyway; (2) the tidal bulge of the Earth is symmetrically both toward and away from the Sun – so, actually, what I’m doing is showing that the equality is fully consistent with the forces calculated from physics:
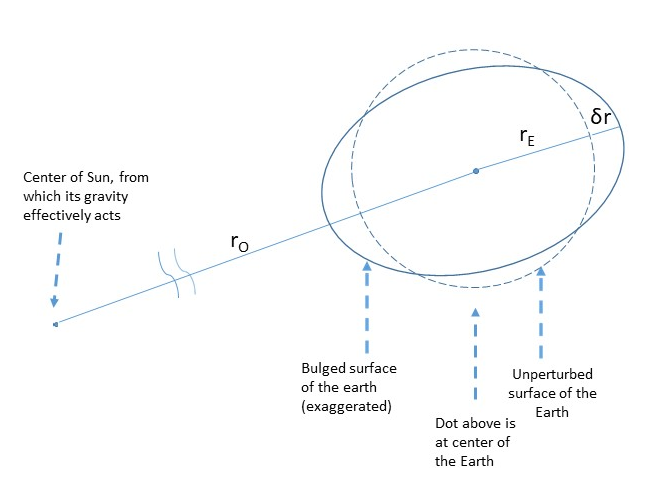
Here, it should be clear:
- rO is the distance between the center of the Sun and the center of the Earth
- rE is the mean distance from the surface of the Earth, where the person is standing, and the center of the Earth
- δr (that’s “delta r”) is the extra distance added by the tidal bulge of the Earth, the same on both sides. I take it as equally large on both sides, which, in fact, is the same result as showing that the weight of the person is the same on both sides.
Also:
- Take M as the mass of the Sun
- m is the mass of the person
- The Earth is rotating about the Sun with an angular velocity ω = (orbital speed)/(orbital radius)
- The bulge stays facing the Sun, which is pretty much exact even if we let the Earth rotate on its own axis. This is as if the Earth is tidally locked to face the Sun in one orientation. Relaxing this constraint to let the Earth rotate makes no difference in the calculations, only making them a bit more complicated. The bulge always faces the Sun, anyway (well, not precisely – there’s a lag)
- G is the universal gravitational constant
For this and another problem in the chapter, I devised an effective potential that combines gravity and the centrifugal force as a function of the distance r from the Earth’s center. NOTE: I use the negative of the potential, for practical reasons during my calculation – fewer triple negative signs to deal with, and possibly lose.
The steps are then:
- Show that the mass (the person) is at the same potential whether on the near side (sunny side) or the far side – that is, the two extremes are on an equipotential surface.
- Show that the resulting force on the person, as the gradient of this potential with respect to the Sun-Earth distance, rO, is (1) normal gravity excluding the Sun’s effect, plus an increment that’s positive on one side (the sunny side, pulling the person up a bit and reducing weight) and negative on the other – that is, in both cases the total force is pulling the person down relative to the Earth (or up in both cases), so that the experienced weight is the same.
Gravity:
- The force exerted on you by the Earth is the same on both extreme sides, at noon or at midnight, as long as the Earth’s tidal bulge is symmetrical, which I won’t attempt to prove here. It works for a spherical Earth and also for an ellipsoidal Earth, and pure symmetry says so. So, we can ignore this constant.
- The gravitational force exerted on you by the Sun does differ at the two locations. Let’s express gravity’s effect as its potential energy, GMm/R, with R being an arbitrary distance from the Sun. Using the notation in the figure,
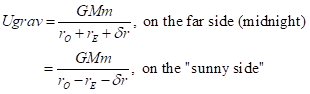
Centrifugal force:
- Ignore the CF arising from the Earth’s rotation. It’s the same magnitude and in the same direction, outward from the Earth, at both extremes (but not at sunrise and sunset, as various people pointed out; we’re not interested in these cases at this time).
- The force is +mv2/r, but it should be recast as mω2r, since the angular frequency of rotation – of the Earth about the Sun – is the same on both sides of the Earth.
- This force can be derived from an effective potential
The force the gradient of the potential, -dU/dr, which is clearly mω2r (after I reverse the sign of the potential). Let’s set this with r=rO, since that’s our geometry.
Deriving the effective potential on both extreme positions on the Earth’s surface:
- On the far side from the Sun, the radius from the center of the Sun to that point on the Earth’s surface is rO + rE + δr.
- Likewise, on the near side, the radius is rO –[ rE + δr].
- Plugging these values into the effective potential, we get:
Let’s expand these expressions to first order in (rE + δr), which is very small compared to rO. We use
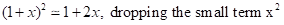
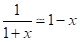, also dropping small terms x2, x3, etc.
Then,
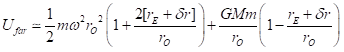
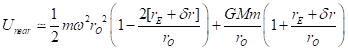
If the potentials are to be the same, we have a requirement that:
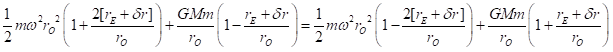
Canceling out the terms that are identical on both sides, we get:
Canceling out the common term rE + δr, we get
That’s just the equation for a stable orbit around the Sun! You can recast it as mv2/r = centrifugal force = the gravitational force between the Sun and the Earth.
So, we have the two points on the Earth’s surface as being at an equipotential of the field from the Sun, including both gravity and the (fictitious) centrifugal force.
What about the force that is provided by the gradient of this potential, 
at the near and far points?
We have
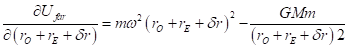
Again expanding about rO:
Here I use r for the whole item, rO (rE + δr). The main terms without the factor rE + δr again cancel, representing the balance of forces between Sun and Earth. We have
The same algebra gives us
That is the forces added by the Sun’s gravity are equal and opposite. Both tend to pull the person a bit away from the Earth’s surface, reducing the person’s weight. Quod erat demonstrandum.
By extension, looking at parts of the Earth bit by bit, the same equality of “bulge forces” acts on the solid Earth, creating bulges that are equal in size on both sides.
Another note: the Moon has a bigger effect than the Sun. Its bulging action simply adds to or superposes on the action of the Sun.
And another note: I use a similar effective potential for the rotating Earth to compute by how much the Earth flattens at the poles and bulges at the equator, just from its own rotation (<– a link).
And: Given that the Earth distorts a bit like a fluid, I also calculated the pressure inside the Earth at various depths, using hydrostatics and the density of the Earth as a function of depth: http://science-technology-society.com/wp-content/uploads/2017/02/What-is-the-pressure-in-the-interior-of-the-Earth_2.pdf. I point out there that the inference of density with depth depends, in turn, upon the estimated pressure at each depth and the effect of that pressure on the rock composition. It’s a self-consistency argument.
The math is not trivial but it is fun.