Sidebar. Integrating the Planck equation over a selected waveband.
Stars act essentially as blackbodies, in the distribution of their electromagnetic radiation into various wavelengths. So do most parts of planetary surfaces – soils, rocks, vegetation (if any), inhabitants (if any). It’s important to know how much energy goes into different wavebands:
- For sunlight / starlight to drive photosynthesis by organisms that are the primary producers, that is, the organisms that capture energy usable by all other organisms by making high-energy compounds such as sugars:
- Only a certain range of wavelengths is usable by these organisms. On Earth the dominant green plants use radiation with wavelengths in the range from 400 nanometers (nm) to 700 nm. Some bacteria can use light down as far as 850 nm. There are very strong reasons from the photophysics of molecules for this restriction, as noted in the text in the discussion of the wonder molecule, chlorophyll. Longer wavelengths don’t have enough energy content per photon to move electrons among molecules. Shorter wavelengths in the ultraviolet can be damaging to DNA; plants synthesize flavonoids and other protectants.
- So, we want to calculate what fraction of the star’s energy at the planet is in the good photosynthetically active region. Really, it’s the number of photons or the photon flux density, which I explain shortly.
- We also want to calculate the flux density of photons in the damaging UV region. Together with the knowledge of the UV-shielding compounds in the planet’s atmosphere, we can estimate a safety margin.
- For thermal infrared radiation, TIR, which is the means by which the planet surface (and all the organisms on it) gets rid of absorbed energy to balance the energy budget:
- There is a total radiant energy emitted, with a flux density proportional to the fourth power of the absolute temperature, I = σT4, and more accurately with an emissivity factor less than 1.0, εσT4. Often, the emissivity is very close to 1.0 so we can just apply a total factor – say, ε = 0.96 for most stuff on Earth, including our own skin.
- Sometimes the distribution among wavebands within the TIR is important. This is critical in calculating the greenhouse effect because the greenhouse gases in the atmosphere all absorb in fairly narrow but important bands. Knowing the emissivities in various TIR bands can also be important in usingTIR fluxes measured remotely to infer the surface temperature accurately. This is readily done on Earth, less so on Mars.
For energy balance, it’s the energy in a waveband that can be absorbed that counts – photons are “weighted” in significance by their energy content, proportional to their frequency or the inverse of their wavelength. A photon of blue light at, say, 440 nm, has 50% more energy than a photon of red light at 660 nm. For photosynthesis, all absorbed photons count the same. A photon of blue light creates an electronically excited state of chlorophyll that within a picosecond or so relaxes to another excited state of lower energy, the same state created by absorbing a photon of red light. Thus, in photosynthesis, it’s the number of photons, not their energy content, that counts. The common measure of radiation for studies of photosynthesis is the photosynthetic photon flux density, or PPFD, quoted in (micro) moles of photons (Avogadro’s number of photons) per square meter per second. For other biophysical reactions such as skin tanning or reddening or mutagenesis for skin cancer or similar effects in plants, the case is similar – the number counts within each narrow waveband, with one or more wavebands for each target molecule in us or other organisms, such as DNA or flavonoid protectants that can be overwhelmed.
We may examine two cases – radiation from the Sun reaching the Earth, and radiation for the much cooler star, Proxima Centauri, our nearest neighbor star, reaching its planet b, or Proxima Centauri b (PCb). This small planet was discovered in 2016 and touted as possibly habitable because the final intensity of radiation at its surface is not too far off what the intensity of solar energy is on Earth.
We may calculate (1) the total energy flux density and (2) the flux density as number of photons per area per second, in the
- UV waveband, especially UVC at 200-280 nanometers (nm), to evaluate the threat to organisms;
- visible waveband, 400-700 nm, which is also the main waveband for photosynthesis on Earth; there is also an extension to 850 nm for minor photosynthesizers, some bacteria; and
- selected thermal infrared wavebands where greenhouse gases absorb to trap outgoing thermal infrared radiation, thus keeping our planet warm.
We need the expression for the number of photons coming off the surface of the star’s surface.
- If you wish to skip to the results, they’re at the very end here.
That law, for a blackbody such as a star approximates well, was discovered by Max Planck. There’s a lot of physics behind the expression for the number of photons per area per solid angle that a blackbody emits, within a small range of wavelengths. It inherently involves the nature of light as quantized into the discrete particles, the photons, where at a given wavelength of radiation all photons have the same discrete amount of energy, hν(“aitch new”) = hc/ λ. Here, h is the universal Planck’s constant, discovered, of course, by Max Planck, ν is the frequency of the light, c is the speed of light, and λ is the wavelength of light. Planck derived an expression that fit observations for the energy emitted per area per solid angle within the range of wavelengths from λ to λ+dλ. Here, dλ is a small increment in wavelength:
![]()
If you haven’t had calculus, this formula might not mean too much to you. Here, T is, of course, the absolute temperature as discussed earlier. Basically, L(λ) is the increment in energy flow from considering a small range of wavelength, dλ. There are several universal physical constants, h, which is Planck’s constant (connected to the finding that all energy is quantized!), c, the velocity of light, and k, Boltzmann’s constant (connected to how temperature is related to energy). These all have fascinating stories of their own, which I won’t go into here. In any case, you can see that a hot star such as our Sun puts out much more energy per area than a cool star such as Proxima Centauri; the total energy output is proportional to the area under the curve for each star.
We can also express the rate in terms of the energy emitted in a range of frequencies between ν and ν+dν,
![]()
For computing rates of photosynthesis (or for DNA damage from UV wavebands) we really want the number of photons, not the amount of energy. Bacteria or plants do photosynthesis with each photochemical reaction driven by a photon, irrespective of its energy as long as that energy is above a minimum (not strictly true, given different degrees of absorption at different wavelengths, but this is a start). The rate expressed in number of photons is this last equation divided by the energy of a photon, hν
![]()
and, back to wavelength terms,
![]()
If we count all photons emitted, over all frequencies (all wavelengths, all energies), we get two expressions familiar in physics. The total amount of energy emitted is
![]()
The factor in front of T4 is the Stefan-Boltzmann constant, 5.67×10-8 W m-2K-4. The total number of photons emitted is
![]()
Here, ζ(3) is a mathematical constant, the Riemann zeta function of 3, with a value of about 1.202 as a simple (pure) number.
Let’s focus on the photon count, not the energy, for those three wavebands. We need to integrate the expression for LP(λ) over the range of wavelengths for each case. There are two basic ways to do this. The first is numerical: Divide the waveband into equal small parts – e.g., 400-410 nm, 410-420 nm, and so on – calculate LP in each small part, add them up, and multiply by the interval Δλ. This is clearly an approximation and it works well only if the interval is short enough that LP(λ) is not changing fast within the interval. It’s easy to program in any language (Python, Fortran, …) or Microsoft Excel. I have two versions of the latter, currently set up to isolate the UV, PPFD (= the visible waveband, also), and infrared. The second version uses finer steps at short wavelengths.
The second route is analytical, using exact mathematical forms derived with integral calculus. The formulas are infinite series, that is, expressions with an infinite number of terms, but the terms converge to a very accurate answer so that only a moderate number is needed. This calculation is presented nicely on one website put up by a commercial corporation, GATS, Inc., of Newport News, VA. They start by converting from wavelength to a new variable, called wavenumber, the number of wavelengths in a meter, 1/λ, given the symbol σ (not the same as the Stefan-Boltzmann constant!). They actually use σ in older units of wavelengths per cm, not per m, but I’ll stay really metric here (really “SI”).
We want to do the integration (this is calculus) over all wavenumbers from a minimum value of σ, which is 1/(850 nm) = 1/(8.5×10-7 m) = 1.176×106 m-1, to infinity. Well, that’s too far, but the number of photons of very high energy (very high wavenumber, very short wavelength) is so small that doing the integral to infinity makes very little difference. After all, we are making a guess about the lower limit that bacteria can use, anyway. The math is shown nicely one of the company’s deeper webpages. The result is
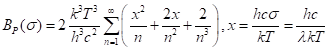
Here, they defined a new variable of integration, x=100 hcσ/(kT). We can do this sum readily because only the first several terms are big enough to matter.
The results
The fluxes reported here in the 3 shortwave radiation bands are, first, in photons per square meter per second at the surface of the star. The next line converts that to moles of photons, with a mole being Avogadro’s number of them, just as for molecules expressed as moles. The line after that is again in moles but projected to the distance of the planet. For this we use the law that the intensity (flux density) falls off as 1/r2 – that is the flux density at the planet is lower than that at the star’s surface by the factor (rstar/rorbit)2. Here, rstar is the radius of the star and rorbit is the radius of the planet’s orbit around the star, taken as closely circular.
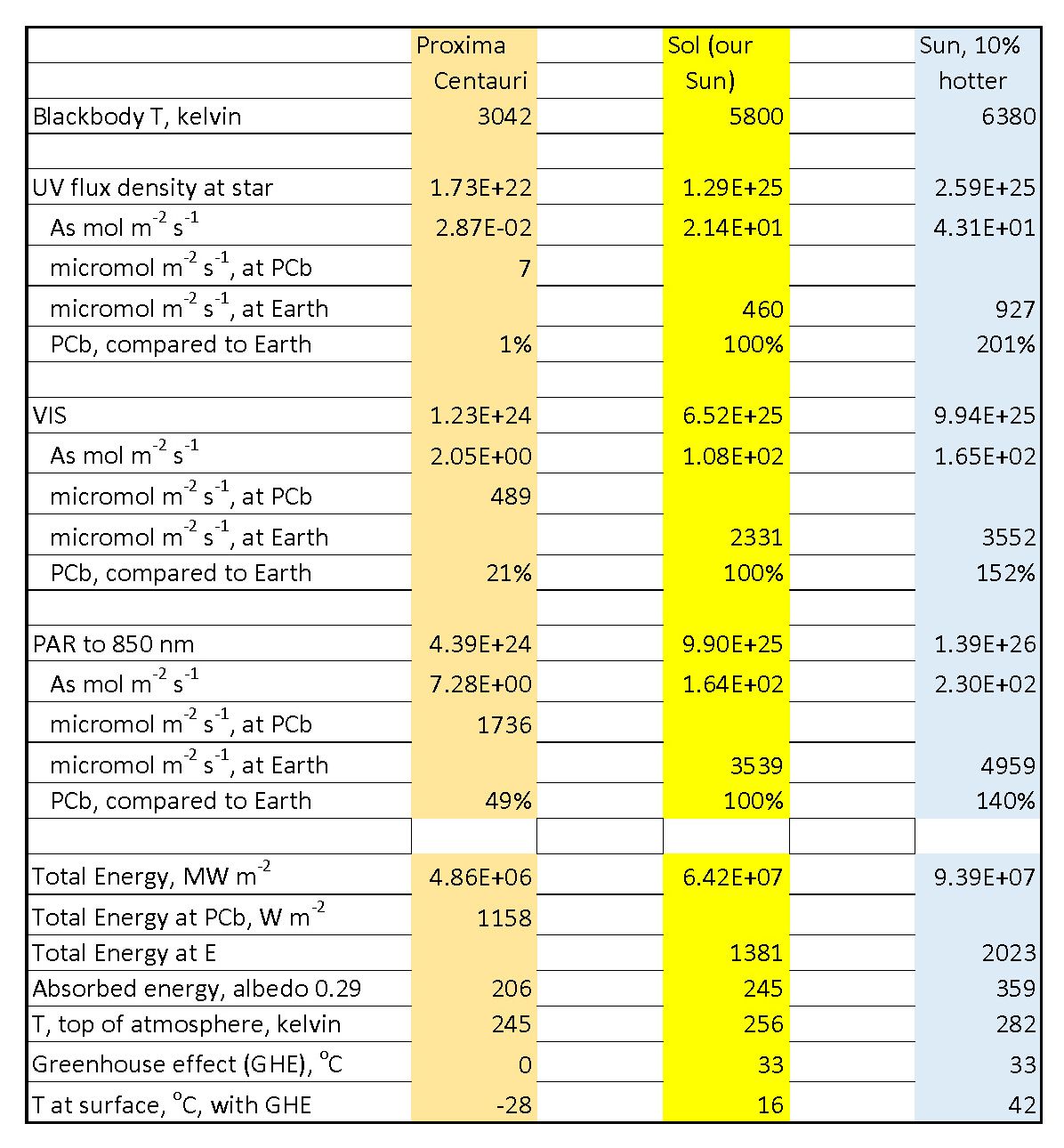
There are notable comparisons.
- The UV flux at Proxima Centauri b is trivially low, only 1% as high as on Earth; a cool star has a tiny fraction of its output at short wavelengths. You would not get sunburned there. You would only get fried by stellar flares and the stellar wind, which also have taken away the atmosphere. Any remanent atmosphere would also condense on the permanently cold side of the tidally-locked planet.
- A 10% increase in stellar temperature from that of the Sun doubles the UV flux (this calculation is approximate). Hot stars are anathema for life, for this as well as for short lifetimes for evolution to occur.
- The visible light on PCb is 1/5th as strong as on Earth, while the 10% hotter star at the same distance from Earth as our Sun is give 52% more visible light. Wear sunglasses, though not as dense as the peril-sensitive glasses in The Hitchhiker’s Guide to the Galaxy.
- If we allow that photosynthetic organisms might use starlight to the longest wavelengths that Earth’s organisms do, then PCb catches up somewhat, getting about ½ as much useful flux density as we do on Earth. On Earth the organisms using the range 700-850 nm are in minor niches, shaded out in general by green plants.
- Going to integration over all wavelengths to get total energy interception, we wee that PCb is not terribly cold, better than Mars (see also the main text about planetary temperatures). a 10% hotter star, alas, would cook us if the Earth were to absorb the same 71% fraction of stellar energy as it does now.
I repeat here a figure from the main text, showing where the energy lies for the 3 stars. Note that the plots are all relative to the peak in the energy. The peak energy for Proxima Centauri is only 5% that for our Sun, and our Sun has a peak that’s only 60% that of the star that’s 10% hotter. If we draw the figure on the absolute energy scale, Proxima Centauri almost gets “lost in the noise.” That’s the second figure, below.