Sidebar: How do we know the mass of a star?
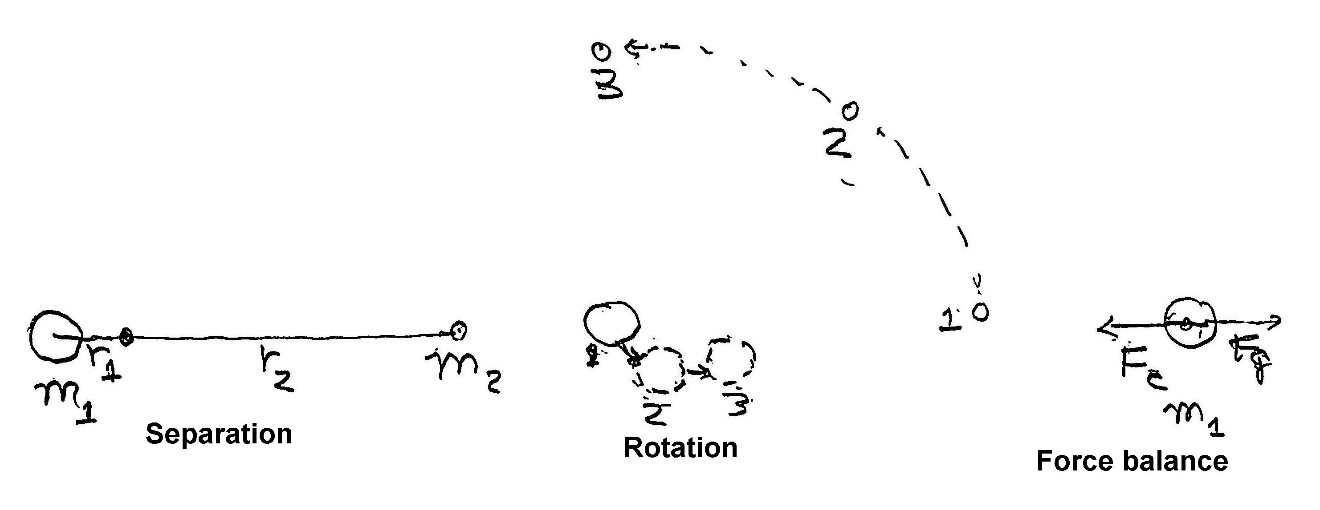
We’ll need some elementary physics for this. It’s easiest for binary stars that orbit around their common center of mass. Fortunately, most stars are binaries, a fact of independent interest. First, we have to know the radius of their orbit around each other. With luck, for nearer stars, we can measure the angular distance between them (call it θ, in radians), and, if we know the total distance, R, we can easily compute their separation, r. Of course, that’s only at one time, and it keeps changing. With luck we can keep observing and get the maximal separation. There’s another constraint, that we need to know the tilt of the orbit. If the orbit is perfectly circular and not elliptical, we’re fine, but with stars in an elliptical orbit around each other it’s the mean radius we want, but we may be seeing only the major axis, the minor axis, or something in between. We can get R if we know the period of rotation. Let’s call that τ (tau; physicists love Greek letters, and a tau won’t get confused with t for ordinary time). There is a virtual force, the centrifugal force Fc that pulls each away from the center of mass. (It’s a virtual force because it’s calculated in a frame of reference that’s moving with the bodies, not an independent “stable” frame of reference. It works perfectly as a calculating device, of course.)
The centrifugal force on mass 1 is Fc1 = m1v12/r12. If this is new for you there’s a nice geometric derivation of this on a page in my website. It’s handy to rewrite this in terms of the angular velocity, ω, which is the number of radians per unit time – that’s how many arcs of length r1 that star 1 takes along a circular orbit of circumference 2πr1 per unit time, or, ω = v1/r1. This is convenient because ω is the same for both stars. We then have Fc1 = m1 ω2r1. Similarly, the force on star 2 is Fc2=m2 ω2r2. The other force acting on both stars is gravity, and it’s equal on the two stars, so, for a stable orbit, the centrifugal forces are equal
![]()
If, say, star 1 is heavier, then r1 is smaller than r2; the mutual orbiting is closer to star 1. In the limit that star 1 is much bigger, then only star 2 moves much and star 1 stays near the center of mass. For a total separation of R, that’s where r1(1+m1/m2)=R, or r1=Rm2/(m1+m2). Right – if m2 is small, r1 is small.
Now look at the force of gravity,
![]()
which is the same on both stars. Now balance centrifugal and gravitational forces on star 2 such that its radius stays constant:
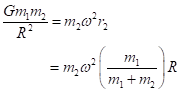
Here I used the converse of the relation between r1 and R to get the relation that r2=Rm1/(m1+m2). Now write out the right-hand side, and you’ll see a common factor of m1m2 on both sides; cancel these out:
![]()
We may have measured the angular velocity via the period of rotation, τ. We can rearrange this equation and substitute ω = 2πR/ τ to get
![]()
This is Johannes Kepler’s law for planets, applied to two stars. The period of rotation is proportional to the radial distance to the 3/2 power. He discovered it over 400 years ago. So, Mars, which is on average 1.52 times as far from the Sun as is the Earth, has an orbital period that is (1.52)3/2, or 1.88 times as long as our own year – that’s 687 of our Earth days. (We won’t get into the interesting fact that the Earth’s rotation period is really one day longer because of the way we define the year.)
We still need one more piece of information to get the total mass and the separate masses. That’s the actual radial velocities, v1 and v2. These velocities might be measured by the Doppler shift in the frequency of light coming to Earth (see, for example, http://www.astronomynotes.com/starprop/s10.htm). This works well if the orbital plane is flat along our line of sight. Figuring out if it’s tilted adds complications we need not go into now. A full circuit of the orbit is a distance 2πR and it’s covered by the sum of the velocities, v1+v2, acting over one full orbital period. We can write this as
![]()
This works for circular orbits. It’s a bit more complicated for elliptical orbits. To continue, we substitute this expression for R to get
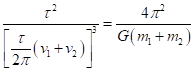
Finally, we get
![]()
We have it now. We have the velocities, we have the period, and the gravitational constant, G, is universal and has been measured in the lab (a long, intriguing story).
Of course, we want the individual masses. That’s easy, with m1v1=m2v2 for a common orbit. From the ratio we can separate the two masses.
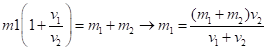
For stars not conveniently in binary systems, there are other ways to estimate the mass from known temperature and brightness, in which stars have been found to fall in uniform patterns. That’s the old Hertzsprung-Russell diagram.