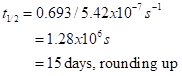The heat that stays
When you burn a fossil fuel, say, oil, you liberate a certain amount of heat. This ultimately dissipates by radiation into space. However, you also liberate CO2, which adds to the planets greenhouse effect and helps trap heat from all sources, including incoming sunlight. Can we compare the immediately liberated heat with the long-term trapped heat?
Direct heat
You’re in a traffic jam on a hot day. As you step out to check out the line of vehicles, you feel the hot emanations from the engines and exhausts. These add to the discomfort. A crowded city with lots of buildings giving off heat or dark structures absorbing sunlight give a similar effect – it’s hotter in the city, by perhaps 5oC or 9oF. Fortunately, the traffic jam dissipates or the city activity slows down at night. The heat disappears.
It actually does disappear, not just diluting into the air. Hotter air, hotter surfaces all radiate more heat than cooler ones, emitting more thermal infrared radiation. We’ll estimate how long the heat hangs around before we look at the trapping of heat by the carbon dioxide released by combustion of the fossil fuel, assuming that that’s what generated the heat from the car or the building.
Direct or sensible heat leaves ultimately by radiation to space
The heat mixes into the air, perhaps part of it also heating a surface. Ultimately, the heat leaves the Earth as thermal radiation… the same as for the heat from absorbing sunlight. With temporary excursions of temperature, the Earth divests itself of received energy by radiating thermal infrared (TIR) photons to space. Radiation is the only way out to space, as there is no heat-conducting medium. So, we must figure out how the extra heat adds to the capacity of the Earth to radiate TIR and, thus, how long it might take to leave the Earth.
Any body (solid, liquid, gas) emits thermal radiation at a rate proportional to the fourth power of its absolute temperature, multiplied by an efficiency of sorts called its thermal emissivity.
First, absolute temperature: it’s measured from absolute zero, which is -273.16oC or -459.69oF. This is a strong concept in physics. It’s been measured, by extrapolating the volume of gases at constant pressure as temperature is varied (I did this teaching a general chemistry lab at Yale as a J. W. Gibbs Instructor). Let’s take a nice air or room temperature, 25oC or 77oF. It has an absolute temperature of 273+25 = 288 kelvin, or 288K (I rounded to the nearest integer).
The rate at which bodies radiate away heat
Second, emission of thermal radiation: There’s a lot to say here, but the important thing in this current exercise is to say that the fourth-power law has been verified in great detail. There is a proportionality factor, sigma (σ), so that we may calculate the power radiated per area from a body as
![]()
Here, the subscript abs reinforces that we’re using absolute temperature, measured in Kelvin. The proportionality constant, σ, is called the Stefan-Boltzmann constant, after two famous physicists who explored radiation, and much more. It has the value 5.67×10-8 watts per square meter per kelvin to the 4th power, or, in the more compact notation, 5.67×10-8 W m-2 K-4. I’m using the practical exponential notation, in which 10-8 means 10 to the 8th power as a fraction, or 0.00000001. You can see why we use exponential notation, not chasing around lots of zeroes and possibly losing some as we write. Also, the ”x” means multiply, so that σ = 0.0000000567.
Not all bodies are perfect thermal radiators. They may have a reduction factor or emissivity, ε, to use in a modified form, P= εσTabs4. Lots of bodies have emissivities near unity, including human skin, most painted surfaces, food, soils, etc. (Some exceptions are bright metals and some special surfaces, which I pose as of great interest for colonizing Mars – see my separate write-up on that, coming soon.) In general we may take ε as close to unity.
OK, let’s calculate the radiated power per unit area from a body at 288K:
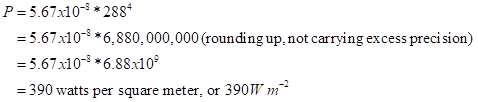
Let’s do a practical comparison, or a few. A good hair dryer puts out 1000 W. Your metabolic heat at rest is about 100 W. Sunlight absorbed on your body can hit perhaps 700 W m-2 on as much as 1 square meter of skin, so that you can absorb 700 W. Hmm. How do you not overheat? You get hotter than the air, typically, so that you radiate more heat; you also cool by evaporation (sweat, water evaporation into your breath).
Stars radiate the same way, but at a much higher temperature, and with radiation not in the invisible infrared so much as in the visible light. The sun’s surface is about 20 times hotter than our 288K, so it radiates at a rate 20x20x20x20 times greater, about 160,000 times greater. It’s at a distance, so that the power is diluted down to about 1371 W m-2 at the top of the Earth’s atmosphere.
How much did your burning of fossil fuel change the temperature of the Earth?
Let’s cut to the chase. You’ve just burned some fuel or otherwise added heat to the Earth, mostly in the air, likely. We’ll measure that quantity in joules (J), but let’s leave the specification very general – just use algebra and call it ΔH. I use the Δ to indicate that it’s a change, an increment over previous conditions.
The calculation from here goes like this:
- That raises the temperature of the air, by an amount equal to the amount of heat, ΔH, divided by the heat capacity of the whole atmosphere – that it, the amount of heat needed to raise the temperature by 1 degree C or 1 kelvin. We’ll figure this out for the whole atmosphere (though this is not necessary as a step).
- The air or the solid surface of the Earth to which the air transfers heat nicely increases its rate of heat loss by thermal radiation. This will be in joules per second, or watts.
- The added heat divided by the increased heat loss rate has the dimension of seconds. It’s basically the time that the heat hangs around (actually, the time for 63% to leave; the loss rate decreases over time as a negative exponential, which we need not worry about now; we just want a time scale).
- We can calculate the extra heat loss rate by computing the rate before the heat release, subtracted from the new heat release rate at the higher temperature. There’s a compact way to express this, using the derivative in calculus. You can skip over the details and see the results, if you wish.
What we’ll find is that the “sensible” heat (capable of being felt from the temperature rise it creates) stays around less than a day.
Here goes:
We’ll do a calculation that does not account for the heat trapping by the CO2. All that happens is that the heat radiates away. After I finished one calculation, I found a virtually identical one by Neil C. Wiles, in his book, The Atmosphere and Ocean: A Physical Introduction.
With an input of heat, ΔH, the temperature of the atmosphere increments by an amount ΔT:
![]()
The heat capacity of the atmosphere is its total mass multiplied by the heat capacity of air per unit mass:
![]()
The product of the density of air per ground area, ρa, and the surface area of the Earth, AEarth, is the total mass of the Earth. Air pressure, about 100,000 pascals, tells us that there is a mass of 10,000 kg, or 10 metric tonnes, of air over every square meter of Earth, on average. (That’s no surprise to a scuba diver, who feels an extra tonne per meter of depth.) The area of the Earth comes from simple geometry, as 4πR2, where R is the mean radius of the Earth, 6371 km or 6,371,000 m; it comes to 5.1×1014 m2. The mass of air is then 5.1×1018 kg. The heat capacity of air varies slightly with water content but is around 1000 joules per kg per kelvin. Thus, the heat capacity of the atmosphere is 5.1×1021 J K-1.
How long does it take for any added heat to leave as thermal infrared radiation?
Next we need to figure out how energy radiates away by emission of thermal infrared radiation. Actually, we want to see how a perturbation, a small increment in temperature, radiates away.
For a body at absolute temperature T, the rate was given earlier, as P = σT4, per area. This formula assumes that the body has an emissivity of 1. The atmosphere definitely does not have this! It’s why the sky feels cold, in the sense that on a clear night you feel quite colder in the open than under cloud cover at the same air temperature. To continue, we consider how much this radiation rate shifts when T goes to T + ΔT. Let’s use the binomial expansion from basic algebra:
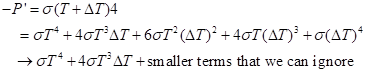
The minus sign indicates that this is a loss. So, the increment in rate of radiative loss is
![]()
Let’s multiply this by the area of the Earth, and also plug in the mean temperature of the Earth for radiation into space, -18⁰C = 255K. We get
![]()
This is the rate of heat loss. The rate of temperature decrease is this, divided by the heat capacity of the atmosphere. I’ll write this as the time derivative (think of it as the small change in ΔT per small increment in time, t):
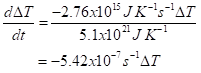
This has the form
![]()
The solution of such an equation is a smoothly decreasing function of time, a negative exponential:
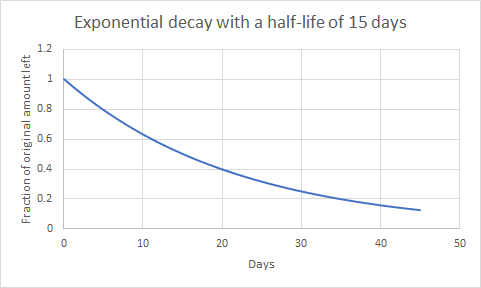
The decay constant value here is k = ln 2/t1/2 = 0.693/t1/2, or 0.0462 per day.
This kind of curve occurs in radioactive decay and other natural phenomena. The characteristic time for decay, the half-life, t1/2,, equals 0.693/k. With our k=5.42×10-7 per second, we get
This estimate agrees roughly with the estimate of 7 days achieved in a somewhat different way (J. A. Curry and P. J. Webster, Thermodynamics of Atmospheres and Oceans, Academic Press, 1999, pp. 409-410), and with the estimate of 6 days made by John Houghton in his book Physics of Atmospheres. So, released heat, by itself, hangs around with a half-life of about 15 days. However, we had to assume that some dense surface with a high thermal emissivity actually had the heat transferred to it, and that this surface did almost all the radiation. The dominant surface is the ocean. We take its heat capacity as that of the mixed layer, about 2. 6m of depth. The heat capacity is 38 times larger than that of the air. That makes the half-life, or mean residence time, about 570 days or 1.5 years. Interesting to think about whenever we put large amounts of heat into the air. However, most of the time the heat went into the air and radiated away from there. We assumed that some body did the radiating. If it had been solid or watery surfaces our estimate is fair, effectively assuming an emissivity of 1. It gets a bit complicated. Air will transfer heat to solid surfaces and to water. On its own, it will also radiate thermal infrared radiation with a smaller effective emissivity. In our fairly dry air in Las Cruces, New Mexico, USA, the emissivity is about 0.6. It takes longer to radiate away.
Net accounting for heat duration, from direct heating
Let’s take an amount of fuel burned. Consider burning 1 kg of a petroleum product, with an empirical chemical formula of CH1.8 (see http://www.law.cornell.edu/cfr/text/40/86.1342-94). This fuel liberates heat (enthalpy) at about 90,000 joules (90 kJ) per gram, so that 1 kg liberates 90 megajoules (MJ). If that heat resides for 15 days we’ll count the effect as 1.35 billion joule-days.
Comparing direct heat and heat trapped by the added greenhouse effect as heat X time
Your combustion activity as adding to heat trapping by what you added to the greenhouse effect
Here’s a sketch of the calculation:
- Calculate the amount of CO2 added to the atmosphere by burning that amount of fuel
- Attribute only 40% of that as staying in the air, with the rest being taken up by extra plant growth and by dissolution into the ocean, in the grand scheme of things
- Calculate the fractional increment in the total CO2 content of the atmosphere
- Multiply that fraction by the amount of warming added per increment of CO2 concentration n the atmosphere. We’ll take the best estimate that doubling CO2 in the air increases the global air temperature by 3°C.
- Multiply that by the heat capacity of the atmosphere to figure out the increment in heat as joules.
- Multiply that by the length of time that added CO2 stays in the air. There are actually a number of processes running in parallel with distinct decay times. Take the shorter time of 250 years, to be conservative.
That combustion of 1 kg of fuel liberates CO2. By the formula above, 13.8 g contains 1 mole of C, creating 1 mole of CO2. From 1 kg, we get 1000/13.8 = 72.5 molCO2. Reduce that to 29 molCO2 because only 40% stays in the air.
Let’s put that into the atmosphere and mix it. We can calculate the fractional increase in the CO2 content of the air. Let’s first get the total number of moles of air, per se:
![]()
Here, AEarth is the surface area of the Earth and ρair is the mass of air per unit area, which is 10,000 kg per m2! The latter remarkable amount is readily calculated the classic formula, F = mg. Take the force per area as the air pressure, about 100,000 Pa averaged over various elevations of the surface. Divide by the acceleration of gravity, 9.8 m s-2, to get a value near 10,000 kg m-2. The final part of the formula above converts from total mass of the atmosphere to number of moles, dividing by the mean molecular mass (“molecular weight”) of air, which is 29 g per mole. We can readily get the area of the Earth, 4πR2, with the radius being closely 6400 km, as 5.14×1014 m2. That’s a few Donald Trump mansion floor areas. The total number of moles is then 1.77×1020.
Your addition to the greenhouse effect
The extra fraction of CO2 in the air is then 29/1.77×1020 = 1.64×10-19. Let’s use parts per million, the common measure of CO2 concentration. Multiply by 106 to get 1.64×10-13 ppm.
How much heat does an extra 1 ppm, say, trap? First, we need to estimate the rise in surface temperature. We get into some interesting phenomena of time scales here. Let’s start by distinguishing the immediate or transient warming from the long-term or equilibrium warming that includes the amplifying or feedback factors (e.g., warming melts some ice reserves, making the planet less reflective of solar energy, thus increasing the solar energy gain). A reasonable consensus figure is that the equilibrium warming is about 3°C for a doubling of CO2 from 400 ppm to 800 ppm, so let’s take the transient warming as half that, or 1.5°C for a doubling. Roughly, the T rise depends on the natural logarithm of (final concentration)/(initial concentration). We’ll write the mean surface temperature of the Earth as a base value, T0, upped by a factor proportional to ln(c/c0), with c0 as 400 ppm.
![]()
Let’s use this to compute the increment in temperature for a small change in c. It’s a bit larger than using a linear approximation, T= T0 + k’(c-c0), as we’ll see. The linear formula would say we gain 1.5°C per 400 ppm, or 0.00375 °C per ppm. Using the more realistic formula, we can take the derivative,
![]()
An increase of 1 ppm out of 400 ppm gives dc/c = 1/400. Now, what is the value of k? When c/c0 is 2, ln(c/c0) is ln 2 = 0.693, and the increment in T is 1.5°C, so, k = 1.5°C/0.693 = 2.16°C. Then, the increment in T from a rise of 1 ppm in CO2 is2.16°C/400 = 0.0054°C.
Our 1 kg of burned gasoline changed the CO2 concentration by 1.64×10-13 ppm. The increase in short-term surface temperature is then this value multiplied by 0.0054°C, or 8.8×10-14 °C. That’s not much, but 1) all our burning of fossil fuels has an additive effect on the CO2 concentration, and it’s huge, 2) a small increment in T stores a lot of heat in a large reservoir such as the atmosphere, and 3) it does have your fingerprints on it, along with the fingerprints of the other 7.6 billion people on Earth that join to make a very noticeable effect.
The amount of heat stored
Here we get into interesting calculations. The surface temperature is that of the solid land surface plus ocean. All the climate models (and measurements) are based on this average temperature. So, greenhouse gas trapping of heat has warmed the air, the land, the ocean surface, each to various depth profiles. Let’s ignore heat moved into land and ocean for now and consider just the warming of the air. The heat stored in the atmosphere for a given increase in its temperature, ΔT, is this increment multiplied by the total heat capacity of the atmosphere, Ctot. This heart capacity is just the number of moles of air (remember these) multiplied by the constant pressure heat capacity of air, about 29 J per mole per °C. The value is then
![]()
The heat stored in warmed air is then
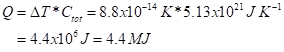
OK, this is much less than the direct energy release of 90 MJ.
Now let’s add in the heating of the land and ocean. That adds some heat storage, but not an overwhelming amount, though it does depend upon the time scale. For solid soil as an example, heat moves in from the surface by thermal diffusion. This is a subject of some detail we need not go into. Suffice it to say that a wave of heat moves in to a mean depth that is proportional to the square root of the time. In a full year, this depth is on the order of a meter, which contains around 1300 kg in good soil, more in rock. At a heat capacity per mass of around 1 kJ per kg per °C, the heat capacity per area of 1.3 MJ m-2 K-1 is significantly less than for the air, at 10,000 kg m-2 * 1 kJ kg-1 K-1 = 10 MJ m-2 K-1. The ocean adds greater heat capacity. Per mass, water has a bit more than 4 times as much heat capacity as air or soil or rock. The mixing depth of the heat is also larger, down to the thermocline (bottom of the layer of warmer water stratified by its higher temperature). The thermocline varies in depth by season and location, and the depth to which mixing occurs again depends on the time scale, so we can use only a rough estimate of a few hundred meters. To a nominal depth of 100 m, the mass of water per area is 100,000 kg, with a heat capacity of 420,000,000 J m-2 K-1. This is 42 times the heat capacity of the atmosphere, so we’re now talking of storing about 185 MJ, nearly 17 times the direct heat release.
If we just restrict ourselves to the heat retained in the air, it’s 4.4 MJ retained by 250 years or about 90,000 days. That’s a heat duration of 4.4×106 J x 9×104 d, or 396 billion joule-days. That, in turn is 396/1.35 = 293 times larger than the direct heat duration.
Going further, and some double-checking
I did omit the ocean heat trapping, which would greatly inflate the trapped heat estimate. Is warming the ocean to the depth of 42 meters consistent with the extra input of radiation from heat trapping, the greenhouse effect? Did I get the oceanic mixing depth wrong? I’ll appeal to the full climate-model calculations. I also took only the transient greenhouse warming into account. That’s only about half of the final warming that comes when warming triggers additional effects, including melting of ice and snow that enables more solar radiation to be absorbed.
We all need to think very deeply about using any fossil fuels! Warm ourselves or move ourselves in cars and we warm everyone much more than we can intuit.