Sidebar: Exponential notation
Very large and very small numbers are difficult to use in ordinary decimal notation. As examples:
* The mass of a proton: 0.000000000000000000000000001673 kilograms.
* The number of atoms in a mole of hydrogen: 602,400,000,000,000,000,000,000 mol-1; here I wrote per mole as mol (no “e”) to the minus 1 power.
* Mass of 1 mole of protons (essentially the mass of one mole of hydrogen, tossing in the electrons, too):
0.00000000000000000000000000167 kilograms x 602,400,000,000,000,000,000,000 mol-1
= 0.001008 kg mol-1
* Wavelength of yellow light (sodium D line): 0.000000589 m
* Mass of the Sun: 19,890,000,000,000,000,000,000,000,000,000,000 kg
* Energy of a photon of yellow light: the formula is (Planck’s constant) x (Speed of light) /wavelength or hc/λ, with Planck’s constant, h, as 0.000000000000000000000000000000000662 joule seconds and the speed of light as 300,000,000 meters per second. That is
J
It’s so tedious to use these decimal representations, and so very, very easy to lose track of the decimal points when multiplying or dividing such large or small numbers. Let the exponent do the work. Consider the mass of a proton. Write down the base as the series of decimal characters that are the first nonzero entries, 1673 (or even 16726… for more accuracy), putting a decimal point after the first nonzero character – that is, 1.673. Then figure out the exponent – how many decimal places to the right is the first character, “1” in this case. It’s 27. So, the number is just 1.673 times the number 0.000000000000000000000000001, which is 1 in 10 to the 27th power. That’s 10 to the -27 power, written easily as 10-27. So, we write the mass of the proton as 1.673×10-27 kg.
For the very large numbers it’s similar. Consider the number of atoms in a mole (of anything). The base it the first run of characters that are nonzero, here, 6024. Put a decimal point after the first character, as 6.024. Now figure out how many decimal places there are after than first character, which is 23. So, we write this number as 6.024×1023.
Doing that next multiplication now looks like 1.673×10-27 x 6.024×1023. Multiply the two bases, 1.673 x 6.024 = 10.08 (with rounding). Multiply the parts expressed as exponents: 10-27 means move 27 decimal places to the right; 1023 means move 23 place to the left; the net is move 4 decimal places to the left:
10.08 x10-4 = 0.001008.
Dividing is analogous. In calculating the energy of a photon of yellow sodium D light, we do the same rewriting:
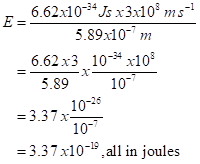
In the last step we subtracted the exponent of the denominator. That’s -7, so we subtract -7: -26 – (-7) = -19.
We can go into what are called significant figures. You’ll notice that, when I multiplied 1.673 by 6.024, I did not write this as 10.078152. I dropped the number of nonzero figures (digits) to 4, as 10.08. That’s because it is assumed in science that you present a number only to the accuracy you claim or to the accuracy you wish to keep. Now, the mass of a proton is known to many more digits than 4, but I’m keeping 4. Avogadro’s number is known to 8 digits but I kept 4. My answer will be kept to the least accurate of the two factors, which happens to be 4.