Sidebar. Equable zones on Proxima Centauri b (not really)
It’s very likely that Proxima Centauri b is tidally locked, with one face of the planet constantly facing the star. The surface of the planet with the star (sun) directly overhead gets baked. The surface facing away from the star cools off to about the temperature of interstellar space, not that far above absolute zero! Are there any places temperate enough for life to exist, even if only as bacteria? We should figure out two things: (1) what is the range of temperatures that bacteria can thrive at, and (2) where these temperatures might be found on the planet.
For the first item, let’s take the range as just above the freezing point of water, near 0⁰C, to the highest temperature on the surface of the Earth where bacteria live, in hot springs such as are found at Yellowstone National Park, say, 70⁰C. I’m discounting very high temperatures, above the boiling point of water (at an atmospheric pressure assumed to be similar to ours, though this is iffy). These temperatures occur only at great depths in oceans. Of course, we don’t even know if this planet has water!
For the second item, I’ll make some simplifying assumptions. For one, I’ll assume that the temperature of a location on the planet depends upon the amount of stellar radiation at that point, plus an increase from a greenhouse effect. This means not accounting for heat being transported to or from this spot by an atmosphere or ocean such as happens on Earth (which is why the poles are not even colder and the equator even hotter than they are). Now, the amount of radiation will depend on the angle between the direction to the star and the normal or perpendicular to the surface (for flat areas). Thus, we’re going to calculate a range of angles that make the radiation not too low, not too high, just right, a Goldilocks story.
Let’s start with the higher temperature, 70⁰C or 343K. How much absorbed radiation will support this as a steady temperature? First, assume that there is no significant greenhouse effect. Oops, that’s not possible. If there’s water, there’s a strong greenhouse effect. I’ll use an Earth-like greenhouse effect that raises temperatures by 33⁰C . So, the radiative temperature of a location should be 33⁰C lower than the surface temperature. Our higher surface temperature of 70⁰C corresponds to a radiative temperature of 37⁰C or 310K. We’ll use the blackbody equation again, I = σT4. We obtain I = 524 W m-2, which is 43% of the direct starlight intensity (see the main text for ways to calculate energy flux density at a planet from the radiative temperature of a star, its radius, and the distance of the planet from the star. The result for PCb is 90% as much for Earth).
This favorable temperature occurs at an angle away from the “sun” of 64⁰.
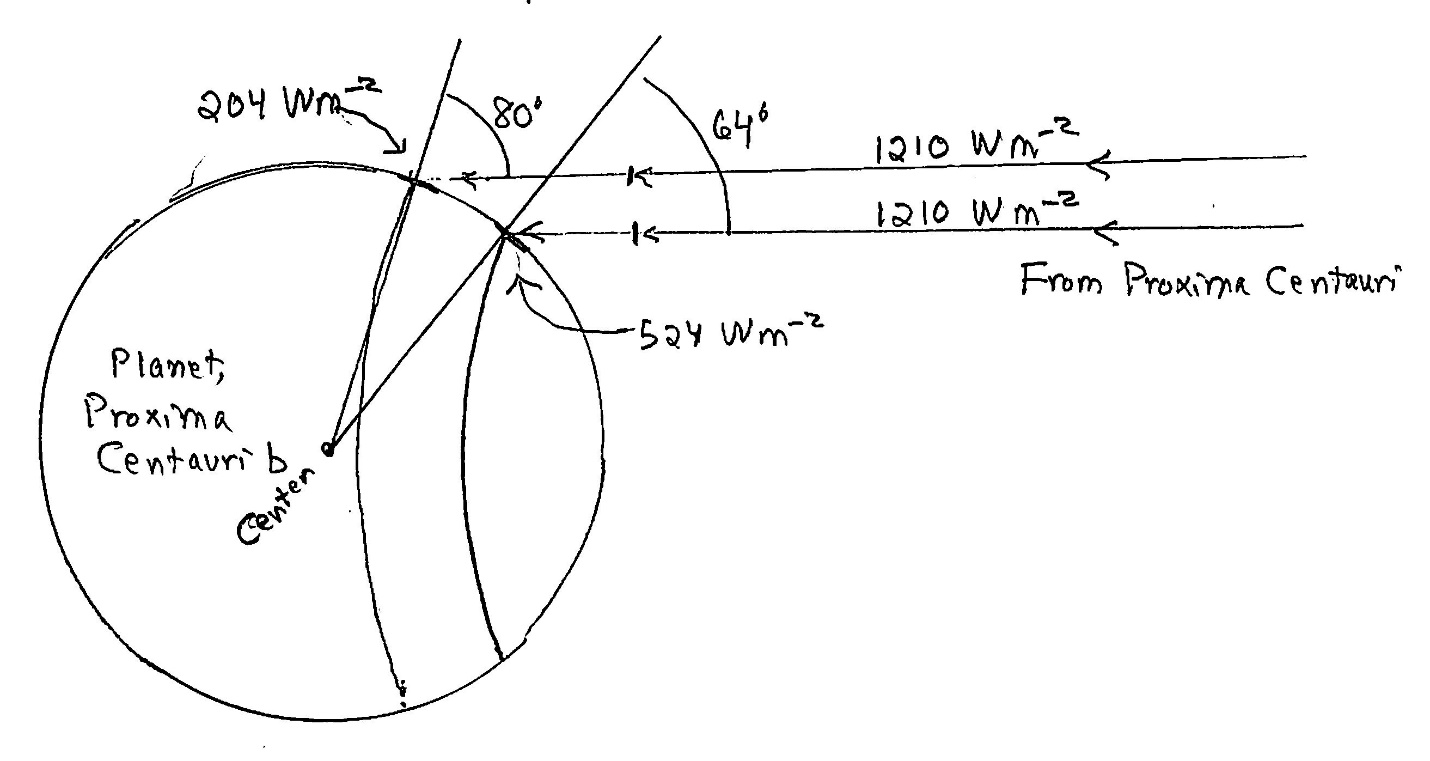That’s over 2/3 of the way, in angle, to the “terminator,” or permanent shadow zone that starts at what we might call the equator. Let’s proceed to the lower temperature. I’ll take this as 5⁰C. Yes, I know that bacteria on Earth are found in areas that get seasonally much colder. However, on a tidally locked planet we don’t expect changeable weather; each location stays around its own constant temperature (except when the star flares!). At a surface temperature of 5⁰C, the radiative temperature will be 33⁰C lower, or -28⁰C, which his or 245K, we need I = 204 W m-2, which is 17% of the full starlight. This occurs at an angle of about 80⁰ from overhead, almost to the planet’s terminator or equator. Overall then, my first estimate is that there’s a narrow band of angles on the starlit side that’s habitable, from 64⁰ to 80⁰. By geometry, we can figure out that this covers a fraction (0.43-0.17)/2 = 13% of the planet’s surface.
The deal breaker is that over half the area of the planet is in low light or zero light. That area is cold. The atmosphere quickly condenses as liquid and solid phases. It’s no longer available to any nascent life forms. Oh, there’s another deal breaker: stellar flares from the red dwarf star.