A black body, in the language of physics, is a body that absorbs all light incident on it. By a principle of physics called microscopic reversibility, this body also emits light of all frequencies or wavelengths. The result is a unique pattern of energy emitted in each wavelength (each color, in visible light, for example). The pattern is universal, depending only upon the temperature of the body.
The Sun is very closely a black body. Most other physical objects, even a book, our skin, or soil, are close to acting like a black body at long wavelengths (in what’s called thermal infrared – obviously not all these look black in the visible range of radiation that in incident on them from other sources, not emitted by them).
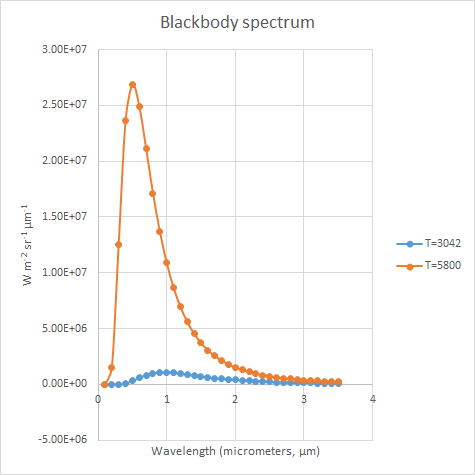
Other emitters are more selective, we may say. A laser is the epitome of this, emitting radiation (light or other electromagnetic radiation) only in a narrow range of frequencies or wavelengths. Closer to everyday experience, fluorescent and LED lights in a home emit light in a few distinct wavelengths or colors, but our eyes interpret the mix as nearly white light. You can split up the light from these lamps with a simple prism or even odd edges of your eyeglasses. Here I reproduce a blackbody spectrum at two temperatures, that of the Sun, near 5800 K, and that of Proxima Centauri, at 3042 K. In astronomy and in much of physics, the measure of temperature is the Kelvin. One Kelvin spans a temperature range of 1⁰C or 1.8⁰F. Kelvin differs from Celsius in starting at absolute zero, where all thermal motion stops and only quantum motion persists.
The values in the graph were calculated from the known equations for a blackbody,
![]()
If you haven’t had calculus, this formula might not mean too much to you. Basically, dI/dλ is the increment in energy flow, dI, from considering a small range of wavelength, dλ. There are several universal physical constants, h, which is Planck’s constant (connected to the finding that all energy is quantized!), c, the velocity of light, and k, Boltzmann’s constant (connected to how temperature is related to energy). These all have fascinating stories of their own, which I won’t go into here. In any case, you can see that a hot star such as our Sun puts out much more energy per area than a cool star such as Proxima Centauri; the total energy output is proportional to the area under the curve for each star. The way that this equation was derived is covered a bit later here.
For comparison, here is the spectrum of a typical LED lamp:
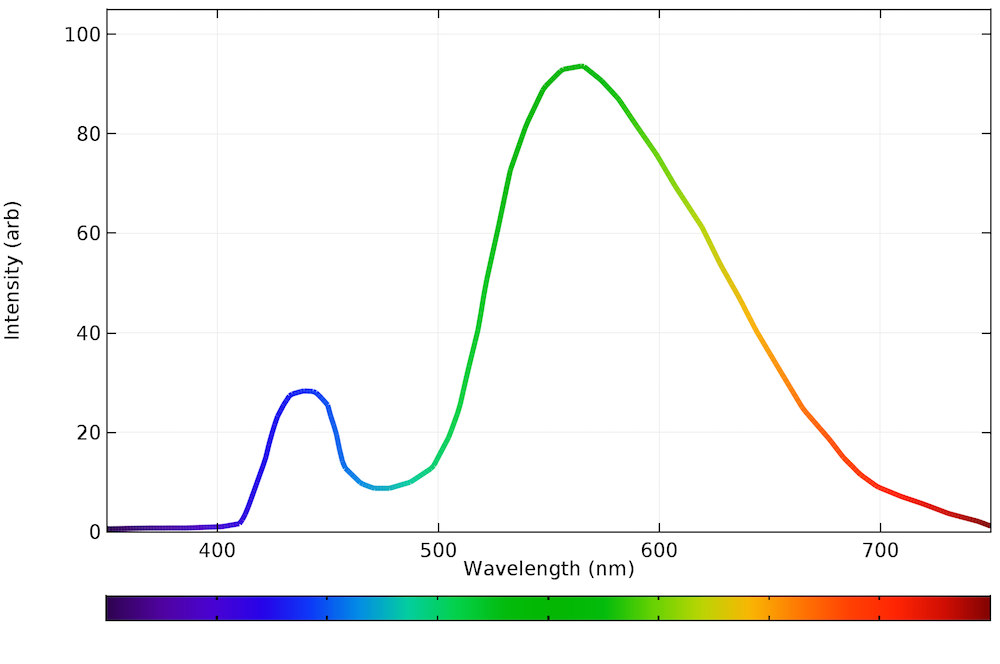
This graph came from https://www.comsol.com/blogs/calculating-the-emission-spectra-from-common-light-sources/.
The fourth-power law for radiation
An interesting and important consequence of this quantum-mechanical law of radiation for a black body is that the rate of emission of energy summed (integrated) over all wavelengths is a simple function of the body’s temperature. It’s often expressed on the basis of power (energy per unit time) emitted pre unit of surface area; there are many ramifications if we consider directions (solid angle) and such, which we need not go into at this point.
It’s a simple law, determined by almost countless observations, that a blackbody emits energy per unit surface area at a rate proportional to the 4th power of its temperature. The temperature of note is the absolute temperature, measured from absolute zero, in Kelvin. The freezing point of water in normal conditions is 0⁰C, which is 273.16K; to get the absolute temperature, add 273.16 to the Celsius temperature. If you wish to work in English units (used now only in the US, Liberia, and Myanmar), absolute zero is -459.69⁰F. So, the absolute temperature in the English system is in degrees Rankine; add 459.69 to the Fahrenheit temperature to get this value.
There is a universal constant of proportionality, the Stefan-Boltzmann constant, usually denoted with the symbol σ:
![]()
Here, I is the amount of energy emitted per unit by per unit area of the body. In international (metric) units, σ has the value and units of 5.67×10-8 watts per square meter per Kelvin to the minus fourth power. Here I’ve used exponential notation, common in science, in which “10 to the power n” (here, n is -8) indicates basically the number of decimal places to move, positive to the left and negative to the right. Thus, 5.67×10-8 is 0.0000000567; similarly, a million is 1×106, or 1000000.
The consequences of the 4th-power dependence of radiation are rather dramatic. An object acting like a blackbody at room temperature, near 25⁰C or 77⁰F or 298.16K, emits electromagnetic radiation (mostly as weak thermal infrared, not light, obviously) at a rate of 442 watts per square meter (W m-2). So, the floor of your home at this temperature emits at this rate. For a square meter (about 1.2 square yards in English units), that’s about half the power of a hair dryer. You don’t feel this because, while you’re absorbing radiation from everything around you, you’re emitting at a similar rate. The net effect of gaining and losing thermal radiation is commonly near zero. You really notice it only in the shade under a clear sky, which emits much less thermal radiation, making you feel colder than the air temperature alone seems to merit. Now consider the Sun. At a temperature T=5800K, it emits 64 megawatts per square meter, or about 145,000 times the rate of that floor. This, or course, is enough to fry anything we make. The density of energy per area decreases with distance, as the inverse of the distance squared, i.e., as 1/r2, where r is the distance from the center of the sun. So, at twice the radius of the Sun, the radiation is only 1/4th as intense. At the distance of the Earth from the Sun, which is 214 times the radius of the Sun, the radiation is down to a mild 1370 watts per square meter when one faces the Sun directly and is sitting above the atmosphere. That’s the right amount to keep our planet at a moderate temperature.
Delving into the history of the concept of a black body is a great place to start when looking into how radiation is created, certainly by thermal sources (as opposed to sources such as electrical arcs, lasers, etc., with very special structures made industrially, or highly “disturbed” structures in nature such as gamma-ray bursters that are life-killers). Physicists around the year 1900 were stymied by the problem of how much light could be emitted by a hot body, and how much of it is at various wavelengths. They considered a model system, such as a cube. Across any one dimension of the cube, one can “fit” waves of radiation (light, etc.) that attain an integer (integral) number of wavelengths across that span. Each mode could be present. This formula predicted the amount of radiation of long wavelengths nicely, fitting the observations on systems that were set up to be as close as possible to black bodies (such as a hollow chamber with a tiny exit hole, at which one could measure the outgoing radiation at any wavelength). However, the integers go to infinity, so there is an infinite number of such modes. If there is no constraint on any of the modes, then there is an infinite amount of radiation with a most of it in radiation of the shortest wavelengths. Given the principle from the mechanics of bodies (which are the emitters) that each mode could have the same amount of energy, the amount of energy present and emitted is also infinite. The very disturbing conclusion was called the ultraviolet catastrophe – meaning that classical physics could not explain the distribution of intensity at all wavelengths.
In Berlin, Max Planck turned his attention to the problem. He ended up making a theoretical testbed, assuming that electromagnetic radiation is emitted in discrete bundles, the photons noted earlier but not suspected to have a real existence (not even named “photons” until later). He then turned to a description of how energy is shared among modes overall – the statistical distribution of energy. The details can be presented in a number of ways, such as in the Feynman Lectures on Physics or in many other texts; we’ll go the end result. Planck started with the principle that there is a total amount of energy, from the Stefan-Boltzmann law relating it to the fourth power of the body’s temperature. He then assigned to each mode an energy E = hc/λ, or using the frequency, ν (the Greek letter “nu”), E = hν. Here, h is a constant, shortly shown to be fundamental in all physical systems – light, vibrating molecules, tumbling molecules, and much more. He then made the total energy come out correctly by saying that the probability that a given mode is present (occupied) is proportional to the negative exponential exp(-hν/(kT). This was familiar from the distribution of kinetic energies of molecules in what’s called statistical mechanics. Making the distribution of occupancy the most disordered (of the highest entropy) for the whole system gave the formula at the beginning of this text.
It was far, far more than a mathematical exercise, not a so-called curve fitting. Planck took it as having fundamental significance. That makes me recall an analysis of our old friend, physicist Barney Ellison: You don’t get credit for being the first one to get an idea. You get credit for taking it seriously. This study of electromagnetic radiation brought in a new fundamental constant of nature, h, which is called Planck’s constant. This finding that all energy is quantized brought Planck the Nobel Prize in physics in 1918 (received in 1919, given that a world war was in progress in 1918). The theory kick-started more remarkable findings, including Einstein’s illumination (pun intended) of the photoelectric effect, one of three great discoveries that won him the Nobel Prize in 1921.
Still, Planck was troubled by the interpretation, a radical break from classical physics. It’s difficult to fathom why nature is quantized, much less to understand a welter of quantum phenomena that we don’t have time for elaboration here – the uncertainty principle, the exclusion principle, quantum entanglement, any of which you can look up. These unique phenomena emerge at small distances and short times, while with larger systems (bigger material bodies, e.g.), the predictions of quantum mechanics eventually match what classical mechanics predicts. The sense of awe at the strange quantum world remains, even with the greatest practitioners of the theory who derived powerful theoretical and practical results from it, the latter including the laser, the ubiquitous semiconductors, magnetic resonance imaging, and much more. The greatest physicist of the second half of the twentieth century, and my most prized teacher, Richard Feynman, said that anyone who understands quantum mechanics doesn’t really understand quantum mechanics! In any event, quantum mechanics “conditions” the properties of everything. Classical mechanics explains the behavior of large bodies such as motors and building materials, given their properties such as material density, stiffness, etc…. but quantum mechanics is at the origin of those properties. A desk resists our hand penetrating the wood, even though the atoms in the wood are mostly empty space, because quantum mechanics disallows our pushing any two electrons into the same quantum state. It’s that fundamental.
Back to applications to how stars emanate energy and end up setting the temperature of the planets around them: At the temperature of the Sun (orange curve in the top figure) there is:
- lots of visible light (also called photosynthetically active radiation or PAR; wavelengths in the range of 400 nm to 700 nm);
- a nearly equal amount of near infrared light (say, wavelengths longer than 700 nm but shorter than thermal infrared radiation… to about 2000 nm or 2 micrometers);
- a bit of ultraviolet (wavelengths between 200 nm and 400 nm);
- and negligible radiation outside the range of 200 nm to about 4000 nm (well, there are still enough photons from the Sun in these ranges to be diagnostic of processes in the outer layers, though not as a noticeable amount of energy delivered to the Earth):
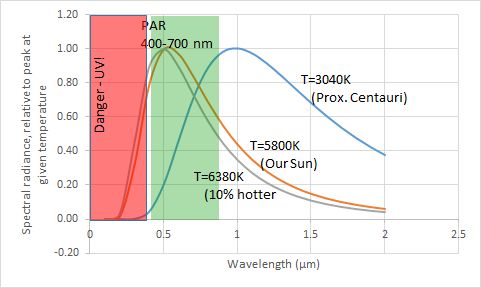
- (The graph differs a bit in form, depending upon our choice of counting up how many photons are in each range or how much energy is in each range.)
So, now we have a means to figure out what kind of light comes out from the Sun and in what quantity. More than that, we can figure it out for a star of any temperature, be it hot Sirius with a surface temperature of 9,940K, even hotter Bellatrix at 22,000K or one of our nearest neighbors at 4.2 light-year’s distance, Proxima Centauri b, with a temperature of 3,042K. Sirius has most of its output in the life-damaging ultraviolet. Its output in the visible range is weighted toward the blue; it really looks blue in the sky. The cool red giant, Antares, is, naturally, quite red in the sky. Some stars look green to us, but no black body (no star) peaks its output in the green. The greenness is a trick of the mind. A nearby red star makes a white star look green by contrast.
This brings up the question of how well stars appear to be black bodies with a well-defined temperature. A hot object emits light as a black body only if it’s packed with internal modes of motion (of atoms, of electrons within atoms) that cover the whole range of energies, hence, the whole range of wavelengths of light. We say that a black body has an emissivity (ability to emit light) that’s uniform across wavelengths. Not all bodies have that. A heated tungsten filament in the old incandescent lamps varies in emissivity from 0.41 to 0.48 across the visible spectrum. It’s not a perfect black body…and, in fact, its average emissivity is less than one-half, making it a rather poor radiator. Polished metals in general have low emissivities. Turning back to the Sun, the deviations from being a black body of a single temperature are modest. That is a bit surprising, since we see light coming from different depths in the Sun that are at different temperatures, as shown by some clever analyses. However, radiant energy from various depths in the Sun’s mass get largely absorbed in the outermost layers, converting it to heat and then yielding the distribution almost wholly appropriate to the very nearly uniform temperature of the outermost layers.