Appendix. Human use of clothing expands tolerable climates
Clothing that covers most of the body is an almost universal practice among humans. Modesty is one driver but thermoregulation is a big driver. Some uses of clothing are obvious – wearing heavy clothing in cold weather, light clothing and clothing that wicks sweat in hot weather. It is not generally appreciated that full-coverage clothing is advantageous in hot, sunny, arid climates. Such clothing does offer a resistance to the transport of water vapor needed for cooling by evaporation of sweat. However, in a wide range of conditions that is not the limiting resistance for cooling – it’s the production of sweat itself that is limiting. The biophysics of it all is developed in chapters 11 and 12 of the book An Introduction to Environmental Biophysics, 2nd Ed., by Gaylon Campbell and John Norman. We’ll work through the most relevant parts but, first, we may take a somewhat broader perspective.
All organisms have a range of thermal tolerance. The most relevant temperature is typically the core temperature, certainly for humans and for all large life forms, at least of animals. (Trees fall into a different category, which will be skipped here, for brevity.) We humans tolerate a wide range of temperatures on our body parts but far less of a range in our thoracic core and especially in our brains. Two degrees Celsius changes in our brain discomfit us and bigger changes endanger us. It is odd that our brains are so sensitive while some mammals and birds are notable for surviving and even adaptively deploying torpor with low body temperatures.
We humans must thermoregulate. Like all other organisms, we can do this by behavior, by use of insulation, and by physiological shifts.
- Behavior: We can move into shade or sun, choose forms of shelter, time our activities to temperature, and the like.
- Insulation: Birds can fluff feathers to insulate themselves. Some mammals alter their fur coats seasonally. We can don clothing of an appropriate type (we can also be stupid and don clothing of an inappropriate type!). The balance between clothing and behavioral choices bears a few surprises. Inuit people from Greenland felt cold in England (so did European-ancestry Americans!). Then there are the Tierra del Fuegians such as the Yaghan who traditionally wore almost no clothing in a cold and rainy climate, much impressing Charles Darwin. They have a high metabolic rate.
- Physiological shifts: (1) evaporative cooling: We and many other vertebrates can cool evaporatively by panting, with dogs being a fine example. We humans have a bigger trick – we can sweat far more than any other animal. That’s why a fit human can ultimately run down any other animal in hunting. Our friend Gilles de Roi in the Galapagos Island used to run down feral goats for food. Sweating is a most valuable part of our thermoregulation in hot conditions. We can easily sweat a liter per hour and some times as much as 4 liters per hour. Of course, only the sweat that evaporates rather than runs off does any cooling. One liter per hour, evaporating, carries away 2.5 megajoules of heat. That’s an average cooling rate of 700 watts, which is more than our maximal metabolic rate at peak exercise intensity. It leaves enough extra to help compensate for radiative energy loading.
- Physiological shifts: (2) rerouting circulation: Mammals, birds, and some fish redistribute blood circulation to stabilize core temperature while allowing peripheral tissues to get hotter, or, especially, cooler than normal. We can reduce skin temperature markedly in the cold. A heron fishing in cold water has countercurrent blood circulation.
The rete mirabile or wonderful net. Countercurrent flow in between arteries leaving warm body and veins returning chilled blood. The recovery of heat is substantial. By the author, 2011.
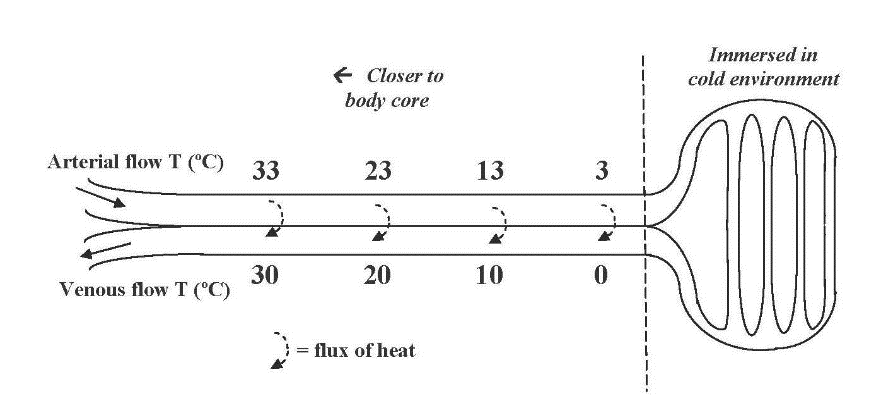
The tuna has a similar countercurrent circulation that lets its core and its powerful swimming muscle stay warm- it is functionally warm-blooded (homeothermic), accounting for its extreme swimming power.
Thermoregulation is all about energy generation, energy interception, and energy unloading. We may take a whole-body total view to explore this, as Campbell and Norman do. We may reprise the environmental conditions:
- Air temperature: consider a fairly hot day, Ta = 38°C
- Solar radiation: a high solar elevation is typical, say, 60° above the horizon for the hot time of day. Fortunately, that limits interception by an upright human to about half of maximum and on a bit more than half the body surface. In clear skies the solar energy flux density is over 1000 W m-2. We may take form-intercepted radiation at up to perhaps 300 W, and averaged over the full 2 m2 of surface that yields an interception of 150 W m-2.
- Thermal radiation: Every surface radiates this, at a rate εσT4 in the blackbody model that works well for all environmental surfaces (no large areas of highly polished metal!). Here, ε is the thermal emissivity, about 0.96 in general for solid surfaces but as low as 0.6 for a clear sky of dry air; σ is the Stefan-Boltzmann constant, 5.67 x 10-8 W m-2 K-4; and T is the absolute temperature. If the surfaces are near air temperature, this thermal infrared (TIR) is 510 watts per square meter. Here, the emissivity factor of 0.96 is applied; emission and absorption have the same factor for any one surface. Bare soil can be much hotter; we have found up to 72°C in Las Cruces, NM, USA, giving a flux density of 771 W m-2! The other half of the body might intercept “cold” sky TIR at an effective temperature 40°C lower than air temperature, giving a flux density of 294 W m-2. If we tone down the soil temperature (with some vegetation) to about 20°C above air temperature we get 653 W m-2 from the ground. The average over the whole body is then 0.5*(653 + 294) = 474 W m-2. That’s not too hot, in fact.
- Windspeed, u, for heat transfer into the body or away from the body: in their example Campbell and Norman (C & N) use a modest 2.5 meters per second, 5.5 mph. This can be varied in any calculation, such as my spreadsheet.
- Humidity: We can specify this as the vapor pressure of water in the air. C & N use 1 kilopascal, appropriate to a relative humidity of 15% at the air temperature of 38°C. That’s reasonable for a hot, dry area. In Las Cruces we have had readings of 2%, though the sensor may have had a hard time working properly at that level.
The energy inputs and outputs to the human are then:
- Input: absorbed shortwave solar radiation. We have this as 150 W m-2, above.
- Input: absorbed thermal infrared radiation. We have this as 474 W m-2, above.
- Input: heat transfer from air to body. This is gtot(Ta – Tb), with gtot as the total conductance of the air boundary layer, the clothing, and the skin as resistances in series, and Tb is body temperature. This is so close to air temperature that it can be ignored in the specific case at hand. C & N calculate the air boundary layer conductance as 0.135 (u/d)1/2, with d as the characteristic dimension of the body. They compound this later with clothing resistance in a final example, and they assume good vasodilation so that the skin transfers heat well.
- Output: emitted thermal infrared radiation. Using body temperature that’s about 511 W m-2.
- Output: heat transfer from air to body – this is accounted under heat transfer from air to body, just changing sign if the body is hotter than the air.
- Output: evaporative cooling. Lungs void air at water saturation. The exact calculation has some subtleties. C & N use a fair estimate that the cooling rate from respiration is about 0.1 times our metabolic heat generation, in non-humid conditions. In the figure of interest below, C & N take a sweat rate of 1 kg per hour as the human special capability.
- Generation: metabolic heat production. This varies with degree of activity. A resting adult human puts out about 100 W total for a rate of 50 W m-2 over two square meters of body surface. C & N consider three metabolic levels, 50, 100, and 200 W m-2. The last figure is for pretty heavy work.
The calculation of final energy balance can be very detailed. C & N collapse it all under reasonable assumptions of conditions to define an effective or operative temperature, Te. It combines radiation load with direct heat transfer:
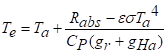
Let’s go through this piece-by-piece. Here, Rabs is just the total rate of absorption of both shortwave and thermal radiation. The other term in the numerator is just the rate of heat loss by the body radiating its own TIR, at a base temperature taken as air temperature. In the denominator CP is the heat capacity of air, 29 joules per mole per kelvin. The term gr is an effective resistance for loss of heat at TIR, presenting the net output minus input as if it were just linear in the temperature difference, gr(Tb – Ta). It’s computed as the rate of increase of TIR radiation per kelvin, or (d/dT) εσT4 = 4εσT3 divided by CP. The term gHa is the aerodynamic resistance of the air boundary layer around the body as noted earlier.
We can finish the calculation. For the stated conditions we get:
- Rabs = 150 + 474 = 624 W m-2
- εσTa4 = 509 W m-2 numerator = 115 W m-2
- gr = 0.225 mol m-2 (Yes, that’s an unusual unit for conductance but it is very useful in plant and animal ecology)
- gHa = 0.39 mol m-2
The addition to Ta is then 115/(29*0.615) = 6.4°C. The operating temperature is 44.4°C. This is just the same temperature of a dark chamber, a blackbody with no sunlight, enclosing the body. It’s above body temperature, and we have to add in the effects of our metabolic heat, but we sweat at rates that readily hit 700 W or 350 W m-2. We survive it, also readily.
Campbell & Norman complete the calculation with a graph, Fig. 13.5:
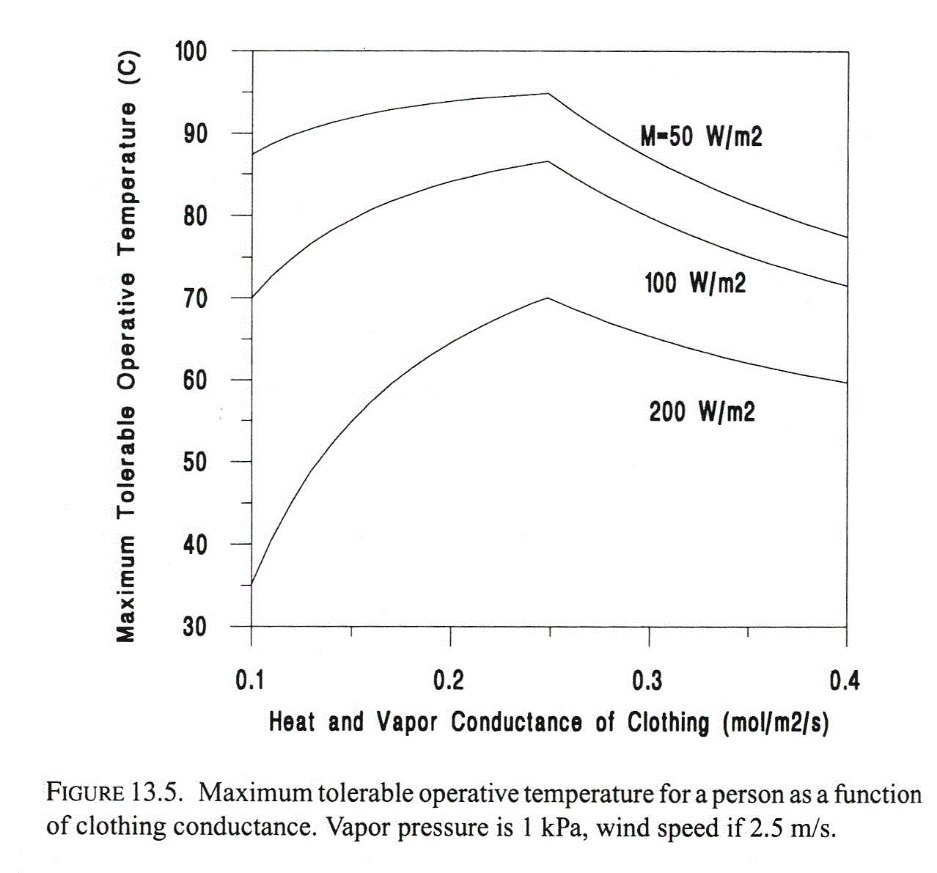
The curves show conditions of stable body temperature as a function of the heat and vapor conductance of clothing. Zero is complete blocking of transport, 0.4 mol m-2 is very light clothing. The three different curves are for three metabolic intensity levels. To note:
- A resting human can tolerate a very high operating temperature.
- High metabolic activity from heavy work reduces the tolerable operating temperature but it’s still high. Talk to a steel mill worker or a boiler stoker.
- There is a break in each curve. On the left side, low conductance limits evaporative cooling by sweating. On the right side, high conductance allows in more and more heat from the air.
- One can make the operating temperature lower by using light-colored clothing to reduce Rabs. (So, why do Tuaregs wear indigo robes? They create their own updrafts from thermal expansion. It’s not ideal but it works moderately well.)
I provide a spreadsheet for anyone wishing to play with the conditions.
Two points I wish to make:
(1) I have taught this concept and its ramifications in my senior/graduate student courses in biophysical ecology at New Mexico State University.
(2) I accept it as trustworthy in practice. Lou Ellen and I began using full-body clothing in hot, dry, sunny game parks of Kenya and other locations. We felt a little warm but nowhere near as warm as if we’d been in short-sleeved shirts and shorts. This calls to mind a demonstration that my beloved teacher, Richard Feynman, used in his famous Feynman Lectures in Physics at Caltech. He had a bowling ball suspended from the ceiling in a lecture hall (Bridge?) At the beginning of the course he pulled the ball up to his face and let it swing away and then back to his face. He said that this showed that be believed in what he was teaching.
Further ideas:
- Tolerance of cold conditions can also be developed. C & N do an admirable job of that, too.
- Inhabitants of hot, sunny areas commonly have dark skin. This increases radiation loading. The clear trade-off is thermal discomfort (or reduced tolerance limits) against the danger of UV damage to skin, including melanoma. Melanoma is slow to develop from UV exposure, so the degree of trade-off is uncertain for me. I had a lot of sunburn as a child in the days before SPF 50, but no melanoma, knock on wood. (Re superstitions: there’s the story of a famous physicist, whose name I have to find. He had a horseshoe mounted over the door to his laboratory. A colleague was taken aback. “Surely you don’t believe in this!” “I don’t, but I hear that it works whether you believe it or not.”)