How fast can a rocket get going in free space (outside Earth’s gravity), as a function of how much of its mass that it burns up as fuel? The answer is interesting. I’ve written an explanation built on an analysis I made for a model rocket taking off from the ground. I get a differential equation, but we can view it as some differentials to be integrated:
The basic equation for a body is Force = F = dp/dt = (d/dt)(mv) (that is, the rate of change of momentum, which is mass times velocity)
We have to be careful – there are two “bodies” – the rocket body and the exhaust gas left behind.
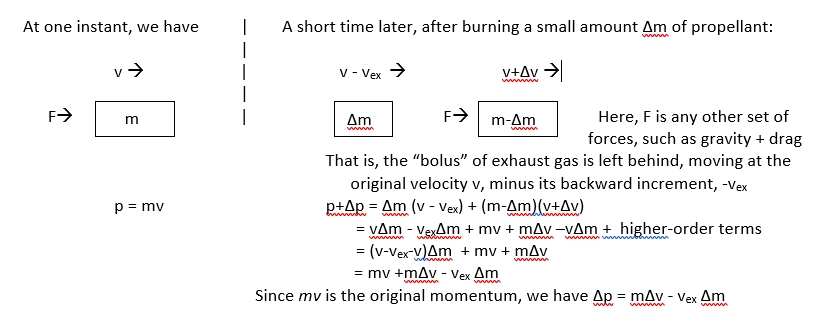
If there’s no external force, F, such as gravity (the rocket being in free space), the change in momentum of the gas trail plus the rocket is zero:
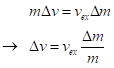
We really should consider these changes, Δv and Δm, as infinitesimals, or
![]()
We’ll do a change of sign here: dm is the mass of propellant lost; the change in the mass of the rocket is the negative of this, so we have
![]()
where we now are tracking the mass of the rocket, mr.
Assuming that the exhaust velocity is constant (the same propellants continue to be burned), this equation can be integrated directly. Assume that the rocket started at a velocity v0 before burning fuel and that its starting mass is m0 and its final mass is mf. The left side of the equation is trivial to integrate, to vf – v0; again, let subscript f denote the final value. Then we use
![]()
where ln is the natural logarithm. We now have
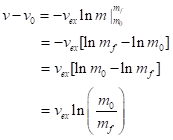
This is interesting. Suppose the rocket burns up half its mass; then, ln(m0/mf) = ln 2. Let it burn up half of what remained, leaving it with ¼ of its original mass. Then, ln(m0/mf) = ln 4 = ln 22 = 2 ln 2, by the properties of the natural logarithm (ln xn = n ln x). Thus, to get to 3x faster, it has to burn down to 1/8 of its original mass. Only by burning to nearly zero can it get going much faster than the exhaust velocity of the gases. Now, the rocket can’t burn down too much; it needs a certain amount of mass (propellant tanks, lines, combustion chamber, nozzle, fuselage…and, obviously, its payload), so let’s say 1/8 of its original mass is the best it can do. It can then get to 3 times vex above its initial or resting velocity.
Clearly, it’s best to use propellants with a high exhaust velocity – undergoing very energetic chemical reactions. I’ll have a writeup about that in a trice. It will include interesting findings about how to match the payload to the desired final velocity by using the right amount of propellant, what the maximal velocity is (when one hits the maximal fraction of rocket mass that can be propellant), how much the need for a fraction of the mass of the rocket to be structural strongly limits speed, how the nature of the propellant chemical reaction energy sets the exhaust velocity, how one can maximize the kinetic energy of the rocket (used in defending against missiles), and at what point in its trajectory does a rocket use fuel most efficiently to create its own kinetic energy (surprise: it has zero efficiency at blast-off and again when it has used up all but 14% of its mass).