Appendix. Mass, energy, and all that
This small appendix is aimed at clarifying a number of concepts integrated into the main discussion of habitability. It clearly can’t be comprehensive in treating the topic of energy, but there are many lengthier and able presentations available for focused studies. The coverage of topics is also not balanced among all the topics in energy; it’s focused on issues brought up in the main text.
The nature of energy – forms, conversions, relation to forces and motion
Energy is the ability to do work – that is, to change the state of motion or position of a system. It takes many forms – kinetic energy of mass in motion, heat or thermal energy in the internal motions of a body such as a piece of steel or sugar or a balloon full of air, chemical energy stored in reactive molecules, electrical energy in currents and in stored charge, magnetic energy (as in the magnetic loops in the Sun), radiant energy as light, thermal infrared, X-rays, etc., elastic energy in a rubber band or blown-up balloon or a watch spring, nuclear energy that can be liberated in fusion or fission, acoustic energy in sound waves or ultrasonic waves (in the range of sounds we hear, very tiny amount of energy).
The forms of energy can be converted into each other, and in the conversions total energy is conserved. At this point it’s useful to discern kinetic energy of motion and potential energy of position in a field. A ball bearing so many meters above a floor has gravitational potential energy, from sitting in a gravitational field. As it falls upon release, it gains kinetic energy as it loses gravitational potential energy, with the sum being conserved (we’ll get to energy lost in air drag). When the ball bearing hits the floor, the initial gravitational energy from lifting it up is gone, and so is the kinetic energy. The energy has now been converted, most likely to thermal energy; the ball bearing and parts of the floor are demonstrably warmer. (Chipping the floor can happen, with energy going into breaking chemical bonds in the cement). The macroscopic energy of motion has gone into increased kinetic energy of atoms and molecules in the ball and the floor.
In the large, systems conserve energy. The sum of potential and kinetic energies, from nuclei to atoms to the Earth, is constant. There are systems that look to be nonconservative, but that occurs when part of a coupled system is ignored for practical reasons. The gain in kinetic energy of an asteroid slung around the Moon looks to violate energy conservation but we may conveniently ignore the relatively minuscule energy extracted from the Moon in the process, so that we do only the dynamics.
The concepts of force, momentum, energy, and power have clear relations, even if the terms are used almost interchangeably colloquially. A straightforward example is provided by a moving mass. Its state of motion is given by its mass and its speed in a given direction. We may add clarity in defining velocity as the directed speed, a vector. The quantity of motion defined by Newton is the momentum, the mass times the velocity, or p = mv. Force is another vector, giving the rate of change of momentum over time. In calculus this is F = dp/dt; the notation is just taking the limit of small changes in p or Δp, over small steps is time, Δt. Energy is then taken as the amount of work (“effort”) done in exerting a force F over a distance. For a constant force over a distance Δx, the work done is FΔx. (In calculus with any arbitrary pattern of force varying with distance, it is the integral 
). There are several compact derivations of the result that kinetic energy then comes out as ½ mv2. That’s for energy in moving in straight lines. There’s also energy in rotation of a solid body. This can be resolved into the kinetic energy of all the parts, using the concepts of moment of inertia and angular velocity. Continuing from momentum and energy we resolve power as the rate of change of energy – e.g., the energy delivered over an electrical utility wire to a home to run an appliance, or the rate of delivery of solar radiant energy to a given surface on a plant leaf. The distinction of power from energy was nicely encapsulated by our friend, R. Clay Doyle of the El Paso Electric Company. He noted that electrical utilities sell power, not energy, even though they bill you for energy. They are required by law to provide energy on the time scale of demand. The rate of energy generation as power must match the rate of energy use by customers, also as power. Similarly, the human brain needs power. A cut in metabolic power in the brain, as from a lack of oxygen, cannot be made up by providing energy later if you die.
An arbitrary number of examples illustrate that, say, chemical energy can be converted into heat, as in combustion, and ultimately into mechanical energy of rocket propulsion or of a reciprocating automobile engine. Chemical energy is quantified in the same units as kinetic energy, joules most usefully in the metric system, comparing the energy stored in the initial state such as two isolated hydrogen atoms moving together to form a hydrogen molecule, H2:
Electrical energy is a potential energy, that of a charged particle in an electric field. Its quantity as a change when the particle or the field changes is the charge measured in coulombs multiplied by the electrical potential, measured in volts. Electrical energy can clearly be changed into chemical energy, as in the electrolysis of water to make hydrogen and oxygen gases.
Radiant energy I restrict here to mean electromagnetic radiation as opposed to streams of material particles. Electromagnetic) energy has a rather different accounting from the energy of material bodies. It consists of electric and magnetic fields oscillating perpendicularly to each other and to the direction of motion:
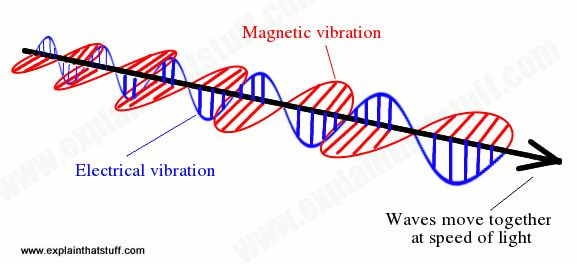
It was unnerving for classical physicists to find that these are waves without a medium; there is no “ether,” rather, there is the vacuum in which photons move. The generation of light isn’t in general described in a useful fashion by resolving the forces, the charged particles bumping into each other such that the acceleration creates radiation much as does the acceleration of charges (alternating currents) in an amateur radio antenna. Physicists count the modes of emission and the population of these modes, or, more macroscopically, by the temperature (and emissivity) of the emitter that acts as a blackbody or by various attributes of, say, electrical spark excitation of a gas as in a neon lamp. The ability of radiant energy to convert to other forms is legend. It can be absorbed to cause chemical reactions such as photosynthesis or the first step in the process of vision or the setting of dental cements. It can simply degrade to heat, as we sense when we’re in strong sunlight.
Thermal energy, or heat, is the most disordered form of energy. As the ability to do work, thermal energy has some subtle considerations. Heat as increased motion of atoms and molecules in a piece of ordinary matter was added by forces acting on the vast number of atomically small particles to increase their kinetic (and potential) energies. However, only some of the energy entered as heat can be made to do macroscopic work such as moving the piston of a steam engine. To extract work heat must be made to flow from a hot body at some temperature (call it Th) to a cold body at a lower temperature Tc. With the best management of expansions, condensation, and heating, only a fraction 1 – Tc/Th can be recovered as external work. (Here, T must be in absolute temperature measured from absolute temperature; that’s in kelvin in the metric system.) We know this from the insightful work of steam locomotive engineer Sadi Carnot. There’s a street named after him in the little town of Aigues Mortes in France. Would that the US would name streets, bridges, etc. after scientists, engineers, artists, and the like, instead of poitical hacks! The efficiency limit exists in all systems defined by temperature, including chemical reactions and even solar radiation. Only part of the energy content in any exchange is available or free energy. It really bugs me that astrobiologists talk about thermal pools on Titan or other celestial body being able to provide energy to support life as metabolic energy. It can’t be done, people.
Old Renault 2CV on rue Sadi Carnot, Aigues Mortes, France
We humans on Earth benefit (mostly) from the atmosphere being a gigantic heat engine. Differential heating of parts of the surface over time and place drive expansions and contractions of air that create wind. The estimated efficiency of wind generation from total solar energy input is 5%. Compare that to global photosynthesis operating at only 0.3% efficiency to biomass embodied energy (plants don’t intercept all the solar radiation, use only the wavelengths of 400 to 700 nm, have internal energy losses to drive chemical reactions forward, suffer damage, etc.). Compare both to the energy use – productive or not! – of the human enterprise, 576 exajoules. That’s 0.016% of annual solar energy interception by the Earth. Wind has its destructive side but circulates water onto land, moderates temperatures, and much more. The energy in wind doesn’t continue to accumulate, of course. It loses energy as internal friction, or viscous losses as it shears (varies with height, especially, so that air “layers” slide across each other). The resultant heat generation just finishes the job of converting solar energy to heat, with the heat eventually being radiated away to space as thermal infrared radiation.
Heat as we commonly experience it shows up in two forms. Sensible heat added to a body – a solid, liquid, or gas – results in a rise in temperature (and the converse, for loss of heat). Latent heat added to or subtracted from a body causes a change of phase -e.g., melting, boiling, condensing, sublimating – without a change in temperature until the phase change is complete. The phase changes of water involve large changes in latent heat content. Steam burns us so badly because of that. The enthalpy (energy) change in steam condensing at 100°C at normal pressure is 8 times as great as the enthalpy change going down all the way from the liquid state at 100°C to a skin temperature of 30°C. The oceans are far more moderate in temperature range, temporally and geographically, than are land surfaces because the phase changes absorb or liberate so much heat. Earth is a watery planet with far more modest temperature swings than dry Mars (though tell that to a Siberian, experiencing 40°C summers and -60°C winters). The latent heat stored in atmospheric water vapor gets released as the vapor condenses into clouds. The resulting warming creates great buoyancy of the cloud-laden air, lifting them to heights that on some occasions called superstorms reach 21,000 meters, into the stratosphere. In times of strong greenhouse heating, such as the Devonian period, this lofting of water that leads to ozone destruction has been implicated in the end-Devonian mass extinction of life.
NASA
There are illustrative examples of chains of energy conversion
The first step in the proton-proton chain for nuclear fusion of hydrogen in the Sun liberates energy as an electromagnetic gamma ray (energy 2.224 MeV), a neutrino of variable kinetic energy and still-uncertain mass-energy, and kinetic energy of a recoiling deuteron. We may follow the gamma ray first. It collides with the many protons and electrons (and a few other nuclei), generally losing both momentum and energy. Electromagnetic energy is thus converted partly into kinetic energy. The particles get hotter and then generate more radiation as they decelerate in collisions (any acceleration, positive or negative, creates radiation). This process is called Bremstrahlung or braking radiation. At the temperature of the Sun’s core, this radiation is of much lower energy than the original gamma ray: thermal energy as kT at 15 million kelvin has a magnitude of only about 1.3 keV. The gamma ray is thus breaking up into many photons of much lower energy. This cascade continues as the photons slowly diffuse out of the core to cooler regions and ultimately to the Sun’s “surface,” where they come out mostly as light with a per-photon energy of just a few eV – a million or so from one gamma ray. Back to the deuteron: its kinetic energy gets converted into energetic photons as it decelerates upon hitting other particles in the Sun or accelerating them – any of the abundant protons or electrons, some other deuterons, etc. The kinetic energy generates many photons, again.
A photon of sunlight leaving the Sun and hitting the Earth can undergo a number of successive energy conversions. Consider one that hits the leaf of a photosynthetic plant (not all plants are photosynthetic; look up saprophytes, e.g.). In a chlorophyll molecule that absorbs it, it creates energy of electronic excitation. A bit of the energy is converted to heat with great rapidity (sub-picosecond time scale). That energy has several alternative fates. One is to jump as (a member of) an exciton of electronic energy to nearby chlorophylls. At one pair of them at the photosynthetic reaction center, the energy is used to separate electrical charge, creating positive and negative ions. It’s now electrical energy. That, in turn, can drive a “dark” (non-light-requiring) chemical reaction to make a strong chemical reducing agent – now it’s chemical energy. There is a network of further chemical reactions that gathers the energy from about 120 photons to form a molecule of glucose from CO2 and water. We might eat that glucose, even directly as the glucose-fructose combo called sucrose, then use it partly for mechanical work of our muscles, partly for more chemical action, and partly for heat. The mechanical work eventually ends up as heat as we pound the pavement… and muscles only convert 28% of their chemical energy input into work, the rest going as heat.
At very high energies, involving speeds that are a significant fraction of the speed of light, the conservation law for energy is extended to the conservation of mass energy (as mc2) and “ordinary” energy such as kinetic energy. The law is exquisitely precise. It equates the change in mass from the fusion of four protons and two electrons to one helium nucleus and two neutrinos to the total energy released as heat and gamma rays.
Any law of conservation reflects a symmetry in the system. In free space, that is, free of electrical and gravitational fields, a force exerted on a body produces the same change in momentum no matter where the body is placed. The symmetry in space gives the conservation of momentum. Conservation of energy is the expression of the equations of motion being independent of time. The equation of motion for a falling ball bearing is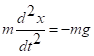 
, where 
is a way to express the acceleration of the body (rate of change of velocity). There is no explicit dependence on time, t. We can start counting time from any point – our stopwatch reading, the UNIX time start (midnight, 1 January 1970), the formation of the Solar System, or whatever. The force of gravity is not dependent on time (or, if it is, it’s because of a volcano redistributing mass on Earth; we then have to include the volcano).
How energy flows.
Heat moves between bodies, or simply out of a body, in several ways. Bodies of different temperatures may be in contact, such that heat diffuses as the randomizing motions of atoms and molecules (in very special circumstances it can also move “ballistically” at the speed of sound). Solid bodies show this relatively slow movement of heat, as when heat moves up a spoon handle. The mean distance moved in simple diffusion varies as the square root of the time; that is, the time needed to move increases with the square of the distance. Moving heat a meter takes a million times longer than moving it a millimeter. This is another good reason for blood flow in us big animals who would otherwise “melt down” almost instantly from internal heat generation. In still water, diffusive heat transfer is “glacially” slow. In soil and rock, heat moves only by diffusion (OK, and a bit by radiation and sometimes by water evaporating and condensing). The daily input and output of heat from sunlight only moves 5-10 cm; the annual input and output moves about a meter. The swings of heat input/output over a century only go about 10 m. Air and water are the big moderators of our climate, with soil and rock having a nearly negligible role (except to ants and our bare feet). Dry Mars with a wimpy atmosphere is condemned to big temperature swings at its surface, as are any future colonists or, at least, their outer wear.
Heat can also move by convection, when spatial differences in temperature generate bulk movement of a fluid (gas or liquid). The common experience of convection is the churning of water heated from below by a heat source, as with a pan of water on a stove. The difference in density of fluids at different temperature creates differences in gravitational forces, acting to move some parcels of fluid up and some parcels down. Bulk movements then transport matter and heat far more rapidly than does diffusion. Convection only occurs in a gravitational field, be it on Earth or in the interior of stars. Wind is large-scale convection. Convection on small scales moves heat to and from plant leaves. In larger stars than life would be able to live by convection occurs from great temperature gradients. There are good summaries of the conditions for convection, such as https://en.wikipedia.org/wiki/Natural_convection (quite mathematical) and https://en.wikipedia.org/wiki/Convective_heat_transfer (qualitative).
Convection is happening on a massive scale beneath our feet. The mantle of the Earth is rock, but it’s hot rock that acts as a very viscous liquid on a large scale. It’s hot, from about 1000°C below the crust to about 3700°C where it abuts the outer core. Some of it is quite low in viscosity, the magma that may erupt as lava, but even the rest of the mantle flows or convects in very large “rolls” or cells. The mantle lies just under the Earth’s tens of km of crust and extends about 2900 km toward the core. Because the mantle is effective heated strongly from below (the core) and is in the gravitational field of the core, it has all the conditions for convection. The heat sources are the radioactive decay of uranium, thorium, and potassium-40, the original heat of accretion of the planet, continued sinking of heavy metals such as iron to the core (releasing gravitational potential energy), and ongoing solidification of the core (releasing latent heat of fusion). Convection gives us plate tectonics, volcanoes, earthquakes, and the cycling of elements between the crust and the mantle, notably phosphorus and carbon important in all living tissue and in the climate system, respectively.
Heat can also move as thermal radiation – a reason that Thermos bottles have mirrorlike reflective coatings. This is a direct conversion from heat to electromagnetic radiation. Movement by radiation is even present inside solids and liquids, though generally less important than is kinetic transfer of heat by atoms and molecules or plasma particles jostling each other. The most important movements of heat as thermal radiation are arguably the radiation of sunlight to the Earth and the emission of thermal infrared radiation from Earth back to space to quasi-balance the Earth’s surface energy budget.
In plant physiology we also resolve the mode of removal of heat by evaporation of water. That’s a case of an intermediate change of phase in the mobile fluid that takes heat away – water changing to water vapor and then convecting away. The reverse can happen when dew forms on the leaf (or the soil, or your car windshield).
Radiation moves by traveling in straight lines at the speed of light. That’s true in the simple case of a vacuum or very diffuse medium. More generally it takes the path of least time or least action, thus changing its effective speed and possibly bending when it meets a change of medium (the old “broken straw in the glass of water” visualization). On meeting various media such as air or a plant leaf, radiation can be scattered into new directions, becoming diffuse radiation such as we receive from the sky apart from the Sun’s disk. Radiation can be absorbed selectively / partially, or transmitted. Absorption creates chemical or electronic energy (or low-energy equivalents) which often become heat. Absorbed by chlorophyll, radiant energy converts to the energy of electronic excitation in the molecule and then mostly to (photo)chemical energy. Absorbed by a photovoltaic cell, light energy becomes in part electrical energy and in part heat.
A stream of sunlight encountering an absorbing medium such as ultraviolet light traversing the ozone layer gets progressively depleted as individual photons get lost. It’s an all-or-none case for the energy of the caught photon. The decay rate with depth is a negative exponential. As a function of total path length, L, and concentration of absorbing “area” per volume the falloff is called Beers’ law – nothing to do with beer per se but named after August Beers. An example is the attenuation of ultraviolet light of various wavelengths by the ozone layer:
Falloff of ultraviolet radiation from the Sun from the top of the atmosphere to the surface of the Earth at noon, for four different wavelengths: UV-A at its longest wavelength (400 nm), intermediate wavelength (350 nm), and shortest wavelength (320 nm), which is also the longest wavelength of UV-B, and UV-C at both 280 and 240 nm. The x-axis is the running fraction of total amount of ozone encountered by depth; it is not the physical depth, since the concentration of ozone is not uniform with depth. The total amount of ozone varies by season and geographic location – consider the infamous ozone hole above Antarctica.
We can derive this pattern by considering that each molecule presents an effective absorbing area or optical cross-section to light. This cross-section is a result of specific energy transitions in the molecule and is not related to the geometric size of the molecule. Beers’ law also applies to the absorption of thermal radiation leaving the Earths’ surface as it travels toward a final destination of space. Each greenhouse gas has it absorption strength (cross-section) at a set of thermal infrared wavelengths. Calculations of the greenhouse effect rely of these intensively measured cross-sections.
Radiation can change in energy content and related wavelength as it encounters matter. This was noted in passing, earlier. A photon can get momentum from colliding with a particle or give momentum to it. This changes its own energy content, and likely its direction of motion. More complex matter than a bare particle like an electron can exchange some of its internal energy with the photon and leave it going on its way. An example is Raman scattering, in which vibrational energy in a molecule is traded with the photon. The Raman spectrum is informative about the molecules in the path.
Kinetic energy moves by collisions, transferring both energy and momentum. The disordered kinetic energy in heat is a particular case in the motion of large numbers of particles. When the moving bodies are charged, the deceleration (a negative acceleration) generates radiation when quantum rules allow it. The energetic deuteron from the first step in the proton-proton cycle in the Sun can generate very energetic photons.
Mechanical energy of macroscopic bodies moves via solid or fluid linkages (driveshafts, pumping of a working fluid in an automobile brake system, etc.). The dynamics of such linkages are a vast subject in physics and engineering. Mechanical energy is readily converted to heat by friction. It can also be converted to gravitational potential energy in pumping water to elevations or to elastic energy in compressing air. Direct conversion to radiation is very specialized, as when unusual crystalline materials are compressed. Direct conversion to electricity can occur with piezoelectric materials that create separated electrical charges upon compression or dilation.
Nuclear energy is an oddity. It does not flow between significantly separated nuclei as does electromagnetic energy between molecules. The strong force is of very short range so that nuclear energy changes occur only with extreme proximity of nuclei, as in the fusion of protons in the Sun. Energy released (or absorbed) in changes of nuclear structure is embodied in kinetic energy of the nuclei and resultant particles (alphas, betas, neutrinos) as they separate (or approach each other) and as often stunningly energetic electromagnetic energy, gamma rays.
Modes of transport of elastic energy, sonic energy, and others cover more topics than can be included here.
Energy is quantized
In everyday life we are unaware that energy comes in discrete packages. It appears that we can add or remove energy in amounts arbitrarily large or small. However, the quantization of radiant energy became very apparent, as in the necessary explanation of blackbody radiation. It became clear that the size of the quantum of energy, radiant or otherwise, was very small, only measurable directly rather recently. It’s 6.62 x 10-34 joules. The same quantization became apparent in mechanics. The earliest instance was in explaining the existence of atoms. Once it was found that the atom is a heavy nucleus surrounded by a number of electrons, there was the quandary that electrons moving around the nucleus are simply electrical charges being accelerated by the electrical (electromagnetic) force. An accelerated charge emits radiation, as is familiar to any amateur radio operator with equipment pushing electrons up and down an antenna. The electrons should orbit more and more closely as they give up radiant energy, spiraling into the nucleus. A pragmatic way out was to postulate that only certain energy states (more generally, states of motion with energy and spatial pattern) were allowed. This worked but the reason was unclear and it did not lead to an understanding of more complex cases of atoms with more than one electron nor molecules with electrons moving among multiple nuclei. An advance was made by Count Louis de Broglie in his 1924 Ph. D. thesis. He viewed electrons as waves (more on that, shortly), or, really, as being guided by “pilot waves”. The waves wrapping around a circular orbit had to meet up in phase each go-round. The wavelength of the waves was taken as inversely proportional to the momentum of the electron, λ = hc/p. The momentum is related to the kinetic energy as KE = p2/2m and the total energy as -KE, with -2*KE as the electrical potential energy. De Broglie submitted a very short Ph. D. thesis. His advisors were reluctant to accept it and give him his Ph. D. degree. They consulted with Einstein, who is reputed to have said something on the order of, “Do it. He may get a Nobel Prize for it.” He did, and they did.
A more comprehensive description came with the Schrödinger equation of wave mechanics (equivalent to the matrix mechanics of Heiserberg). For a steady state of a system such as an atom, this equation solves a differential equation for the amplitude of a wavefunction, ψ, over all space. It is a complex number. Its magnitude ψ ψ* (the star means with the imaginary part reversed in sign) gives the probability of an electron being at the chosen position. There are complementary forms for the probability of the momentum. Yes, it is probabilistic, with the probability of a system being in a given state “collapsing” to a definite outcome only upon measurement. There are many other features of quantum mechanics that you may be interested to look up, including quantum entanglement, the paradox of Schrödinger’s cat that’s in a superposition of states of being both dead and alive, and tunneling of particles through barriers for which they don’t have enough energy in classical mechanics.
The waves appear to reflect reality. Particles of light, the quantized photons, also act as particles. They carry momentum and can kick material particles to change the particles’ momenta. Their momentum that they carry is small relative to the energy that they carry. Still, there are designs for ultralight spacecraft that will be accelerated by the momentum of sunlight. Conversely, material bodies also act as waves. We have de Broglie’s formula for their wavelength, λ = hc/E, in terms of Planck’s constant, h (derived for light!), the speed of light, c, and their kinetic energy, E. Electrons sent through a crystal with its regular spacing of atoms get diffracted just light does! They also show interference patterns in the classical two-slit experiment. Weirder yet, electrons interfere with themselves! They can be sent through the slits one at a time and still yield the interference pattern. Richard Feynman, my favorite teacher, describes particles as taking all possible paths from A to B at once, while only those paths with similar integrated action reinforce each other to give the impression of a single trajectory. Quantum mechanics has such amazing stories.
There was more to come in quantum mechanics. In atoms having multiple electrons, it became clear that the electrons could not all settle into the lowest energy state. In the simple picture of an atom, there are discrete energy states, starting with the lowest state called 1s, the “1” being obvious and the “s” meaning symmetric for the spatial pattern of the electron’s probability distribution around the nucleus. The next higher state is 2s, and, again in the simple picture, three states of (nearly) the same energy but with lobes of electron distribution poking out in three spatial directions, x, y, and z. These are the 2p states. Next are the 3s, 3p, and 3d states, with the last having a more geometrically complicated pattern in space. The states of energy and spatial distribution are filled in order. Thus, the H atom has one electron in the 1s state, the helium atom has two atoms in the 1s state, but the lithium atom has two electrons in the 1s state and one in the 2s state. Its electronic configuration may be written as 1s22s1. Enrico Fermi postulated his famous exclusion principle, that any two particles like electrons cannot be in the same state. Therefore, the third electron can’t go into the 1s state. In helium there are two electrons in the 1s “mode,” but one electron is in the 1s state with its spin pointing down, the other in the state with its spin up (how a point particle can have a spin is beyond the scope of this discussion!). Particles with spin angular momentum that is an odd multiple of the base, h/2π, follow this rule, and we call them fermions, for obvious reasons. The other type are bosons, named after Satyendra Bose (and Albert Einstein). So, following the rules, we may look at aluminum, element 13. Its electronic configuration is 1s22s22p63s23p1. On consequence of the Fermi exclusion principle is the hardness of matter. When I push on a desk, the wood or plastic resists firmly. I’m trying to push electrons together but they forbid being pushed together into a low energy state. Only a higher energy state is possible.
Most of our us and of our environment is composed of molecules, atoms bound together (OK, a single xenon atom is also considered a xenon molecule, but that’s a rare case). The pragmatic picture of chemistry is that the atoms in a molecule share electron density between them. The wave mechanical picture is more sophisticated while expressing very similar concepts. In 1927 Linus Pauling at Caltech used very simple approximations to the wavefunction of the H2 molecule as two molecular orbitals. He calculated the binding energy relative to the two free H atoms that was half that of reality. Modern QM calculations using density functional theory often appear to exceed the precision of measurement.
Mechanical motion is quantized. We may consider the simple carbon monoxide molecule. I chose it for its simplicity as well as for its having a separation of charge, a little negative on the oxygen and a little positive on the carbon. This makes it responsive to electromagnetic radiation that can jiggle the charges, resulting in absorption (or emission) of radiation, a topic in the next section on excited states and transitions.
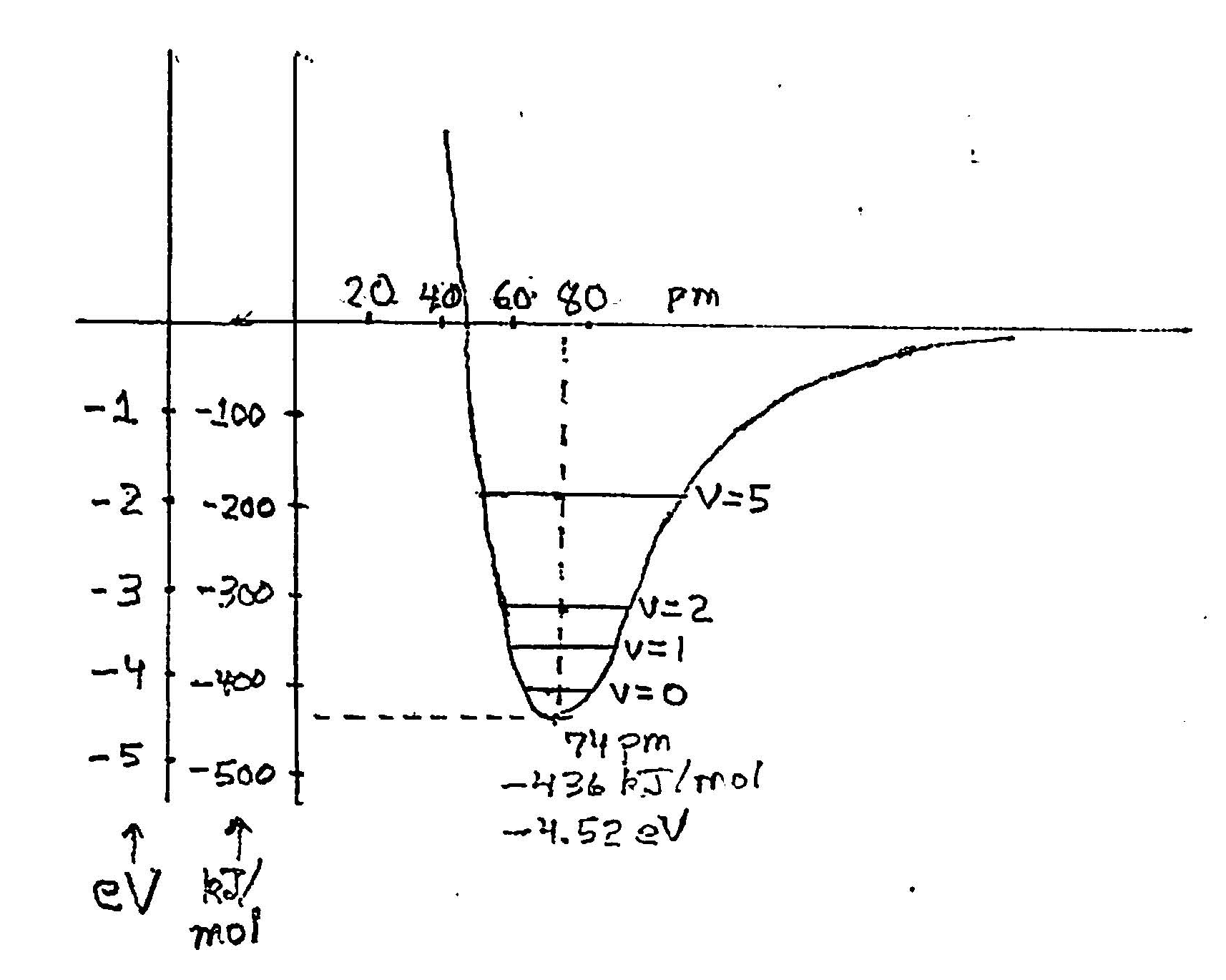
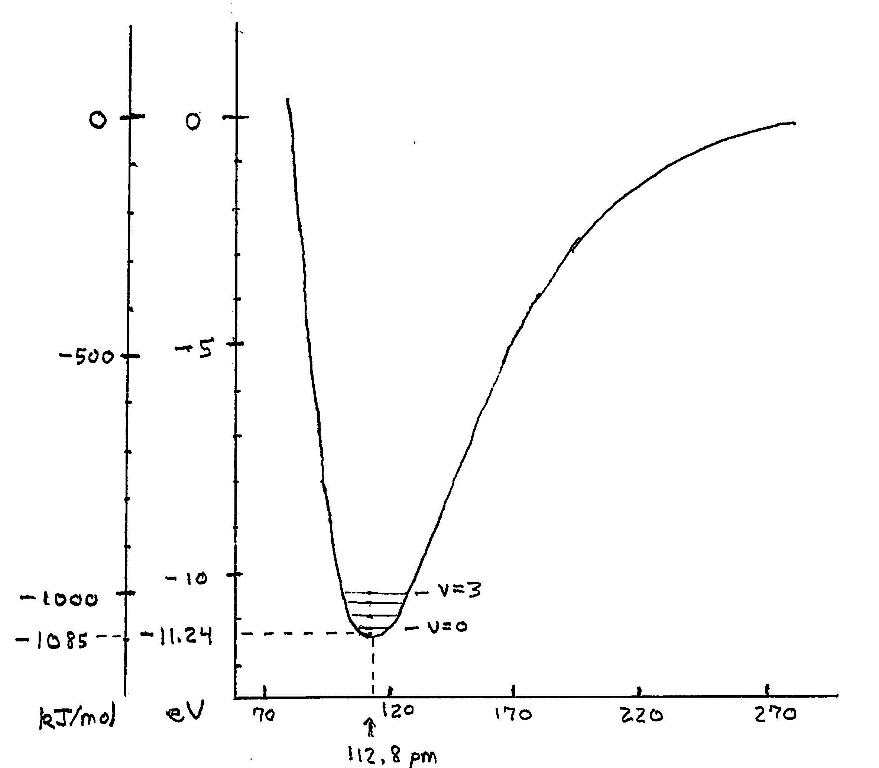
We can calculate the potential energy of the C and O atoms at various distances apart. We ordinarily assume, to very good accuracy, that the electrons adjust their state of motion to any placement of the nuclei. We get a curve of the same shape as for the H2 molecule, differing in energy and distance scales: The binding of CO relative to C and O atoms is 11.24 eV, compared to 4.52 eV for the H2 molecule, and the distance for lowest energy is 112.8 picometers vs. 74 pm for the H2 molecule.
At large distances the potential energy is small, becoming strongly negative and reaching a significant depth or binding energy at the nominal rest position of the atoms. Moving closer, the binding decreases are then reverses to repulsion, dominated by the strong repulsion between the positively charged nuclei.
In classical mechanics, the atoms could be placed at any separation and with any state of motion – any momentum. In quantum mechanics this is not so. Placing the nuclei at a fixed position, such as the energy minimum, would give them infinite uncertainty in momentum. The steady state of minimum energy is near the zero point but above it. The condition for the steady state involves the right behavior of the wave packet describing their motion at the two endpoints of the motion. These are the sides of the potential well at the line marked v = 0 for the ground state:
Other steady states of this vibration lie at progressively higher energies.
Excited states and transitions.
In classical mechanics each way of moving for a molecule has on average an equal amount of energy, ½ kT, where k is Boltzmann’s constant and T is the absolute temperature. The CO molecule has three translational degrees of freedom, two rotational degrees of freedom in two orthogonal directions, and one vibrational degree of freedom. At terrestrial temperatures the translational and rotational modes all have that much energy, averaged over many molecules. The vibrational mode is “frozen,” in contrast. It takes too much energy to move a CO molecule from its zero vibrational quantum number, v = 0, to its first vibrational quantum number, v= 1. In statistical mechanics, the probability of an energy state being occupied is proportional to the negative exponential of the energy, divided by kT: it is exp(-E/kT). The vibrational energy added in the transition from v = 0 to v = 1 is 4.26×10-20 joules. In comparison, the average thermal energy ½ kT at room temperature, 300K, is 2.07 x 10-21 J, a factor smaller by a factor of 19.4. Then, exp(-E/kT) is 0.000035; on average, on molecule in 28,000 is in the v = 1 state. This freezing of the vibrational energy mode is manifested in macroscopic phenomena: the heat capacity of CO gas does not have a contribution from vibration until the gas gets very hot. We may add this to the phenomenon that atoms exist at all to the effects of quantum mechanics on everyday life.
The CO molecule can be excited into the v = 1 vibrational state, and higher states, by absorbing light. That happens provided that the photon energy very exactly matches the energy of transition (energy is conserved, again). We calculate the wavelength of that light from E = hν = hc/λ. We get λ = 4.7 μm or 4700 nm. That’s in the infrared regime. The example of CO is useful but CO is only abundant around industrial combustion sites, including vehicles, and vegetation fires. Carbon dioxide is quite abundant and getting more so. This is true as well for methane, CH4, and nitrous oxide, N2O. They have their characteristic vibrational energies and thus their characteristic wavelengths of absorption. Absorption of light to change the vibrational state generally excites concurrent changes up or down in rotational energy, so that there are numerous wavelengths of absorption, more or less filling a band. Quantum mechanics lets us calculate the strength of the absorption as well as the energy or wavelength.
The converse process occurs. The vibrationally and rotationally excited molecule can give up its energy and release a photon. The strength of emission and the rate (as well as it related lifetime) can also be calculated. With more energetic photons, electrons can be kicked into higher energy states in what we term rovibronic transitions.
Physicists find the concept of energy incredibly powerful, useful in understanding phenomena at all levels. Yet it has its philosophical challenges. As Feynman said…
“Comprehending energy at its most fundamental level isn’t easy. In the famed Feynman Lectures on Physics, Vol. I, p. 4-2: “It is important to realize that in physics today, we have no knowledge of what energy is. We do not have a picture that energy comes in little blobs of a definite amount. It is not that way. However, there are formulas for calculating some numerical quantity, and when we add it all together it gives us “28” – always the same number. It is an abstract thing in that it does not tell us the mechanism or the reasons for the various formulas.”
This, from a Nobel Laureate with a supreme command of physics. (He also said that, if anyone claims that [he] understands quantum mechanics, [he] doesn’t understand quantum mechanics.) So, in the full conceptual development of energy, we have exquisite formulas without a concrete object without a particle we can point to and call energy. Let not yourself be troubled about the deepest issues; use the, formulas with their elegant understanding that’s just a bit short of a final comprehension. This philosophizing reminds me of a section in the very informative and very humorous book, Chocolate, the Consuming Passion, by Sandra Boynton. In a passage about the philosophical ruminations about the chocolate, including how we know it exists (philosophers do such things), she adds that the capitalists realized that it doesn’t matter if chocolate exists, as long as people will buy it.